斐波那契数 & 算法的评估 & 时间复杂度的估算 & 大O表示法 & 斐波那契数复杂度分析
算法
算法是用于解决特定问题的一系列的执行步骤。如:
例一
使用不同的算法解决同一个问题,效率可能相差非常大。如:求第n个斐波那契数。
👉 斐波那契数列又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、…… 在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*)。
方式一:
打印结果:
从打印结果可以看到,第1、2、3、4个斐波那契数能够正常打印,而第64个斐波那契数却无法正常打印。
方式二:
打印结果:
算法的评估
事后统计法
如果单从执行效率上进行评估,可以比较不同算法对同一组输入的执行处理时间,这种方案也叫作:事后统计法。
- 优点:
从执行处理时间可以直观的看出来算法的优劣; - 缺点:
执行时间严重依赖硬件以及运行时葛总不确定的环境因素;
必须编写相应的测算代码(Times);
测试数据的选择比较难保证公正性;
使用自定义工具 Times 查看两种实现方式的执行时间:
打印结果:
从打印结果可以看到,fib1 是非常耗时的,而 fib2 在同样的数据条件下,执行时间基本为0。
算法的优劣
一般从以下维度评估算法的优劣:
- 正确性、可读性、健壮性(对不合理输入的反应能力和处理能力)。
- 时间复杂度(time complexity):估算程序指令的执行次数(执行时间)。
- 空间复杂度(space complexity):估算所需占用的存储空间。
时间复杂度
时间复杂度:在计算机科学中,时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。
大O表示法
一般用大O表示法来描述复杂度,它表示的是数据规模 n 对应的复杂度。
大O表示法:算法的时间复杂度通常用大O符号表述,定义为T[n] = O(f(n))。称函数T(n)以f(n)为界或者称T(n)受限于f(n)。 如果一个问题的规模是n,解这一问题的某一算法所需要的时间为T(n)。T(n)称为这一算法的“时间复杂度”。当输入量n逐渐加大时,时间复杂度的极限情形称为算法的“渐近时间复杂度”。
使用大O表示法时会忽略常数、系数、低阶,如:
👉 注意:大O表示法仅仅是一种粗略的分析模型,是一种估算,能帮助我们短时间内了解一个算法的执行效率。
对数:8 = 2^3 -> 3 = log2(8)、16 = 2^4 -> 4 = log2(16)
对数阶的细节:
对数阶一般省略底数,如:log2(n) = log2(9) * log9(n),省略常数项后就是 log2(n) = log9(n),所以 log2(n)、log9(n) 统称为 logn。
示例:
常见的复杂度
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)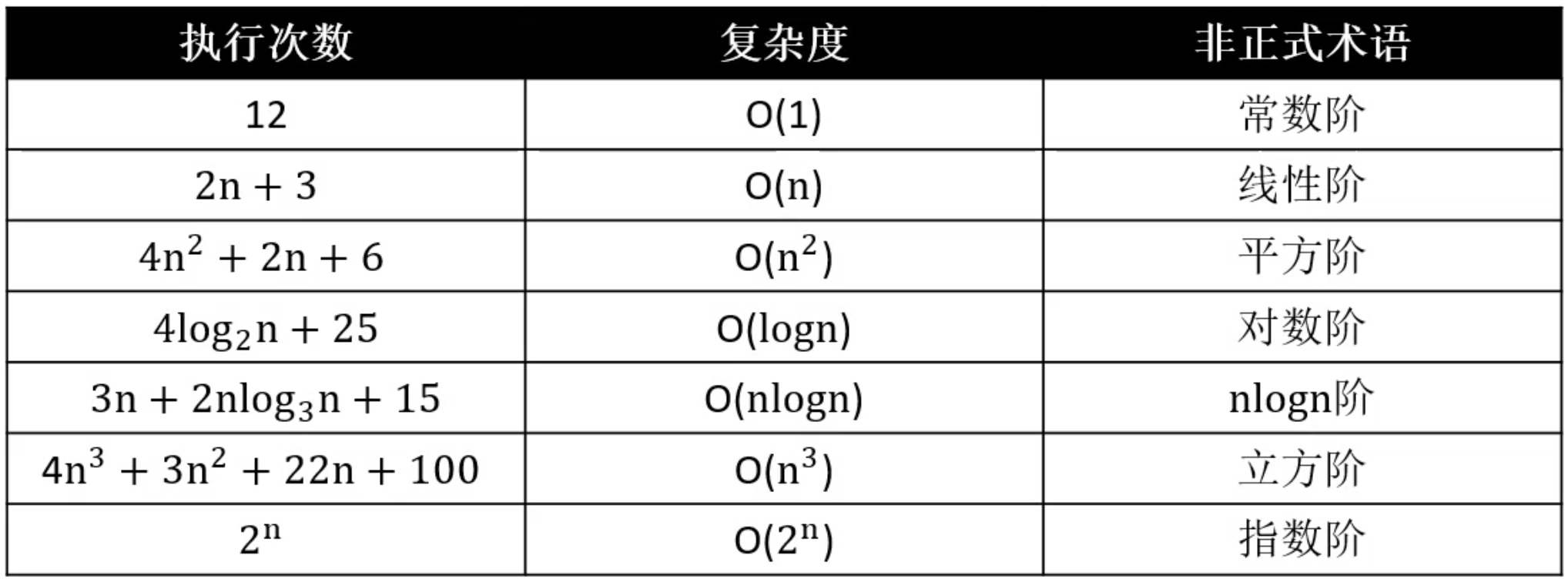
使用函数图像绘制工具绘制 log(n),n,n*log(n),n^2,n^3,2^n:
数据规模比较小时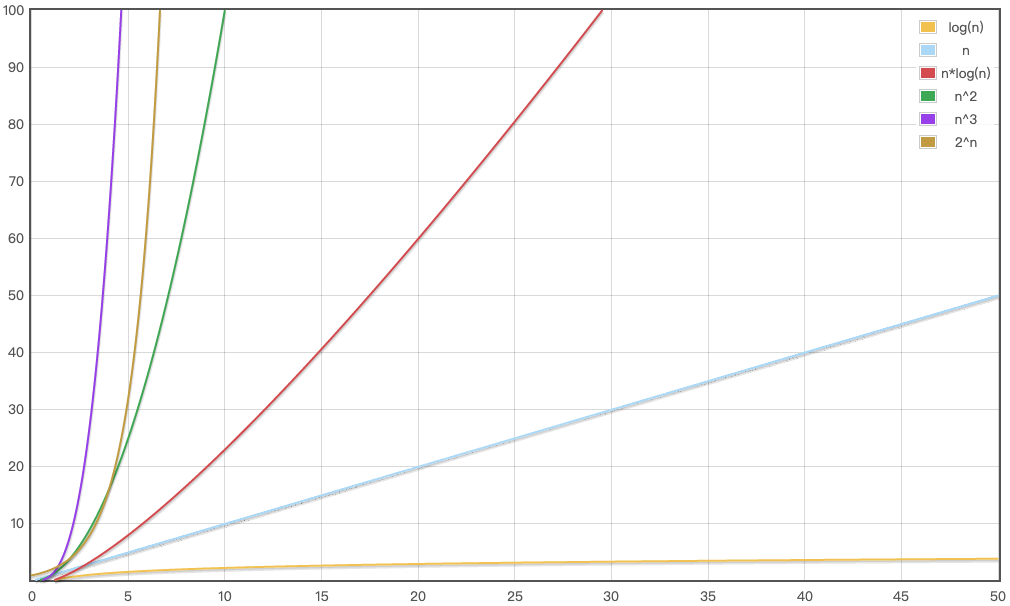
数据规模比较大时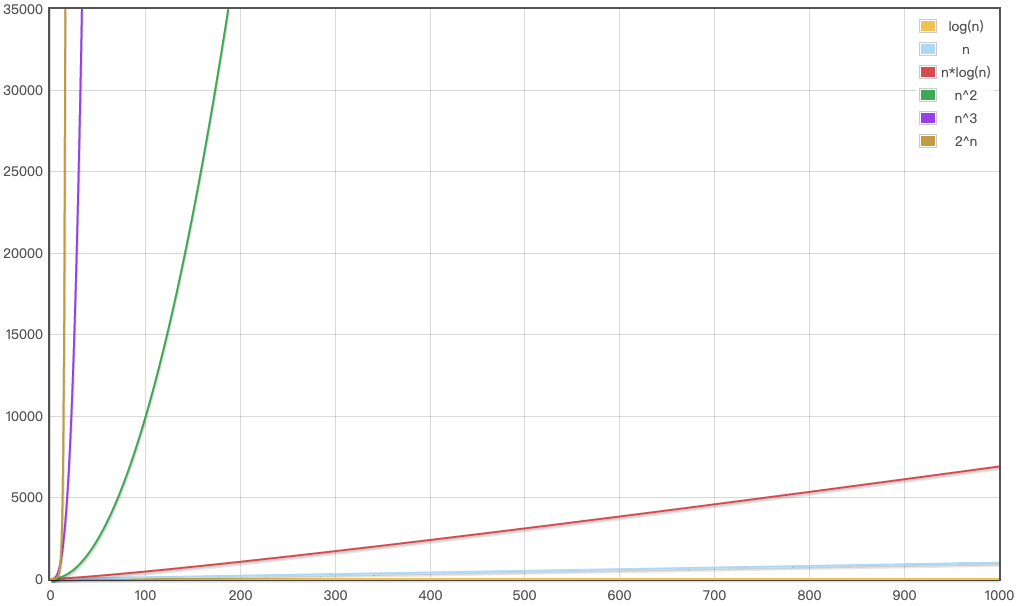
多个数据规模的情况
|
|
空间复杂度
|
|
例一的时间复杂度
|
|
在 fib1 中,如果 n = 5,那么结果就是:1 + 2 + 4 + 8 = 2^0 + 2^1 + 2^2 + 2^3 = 2^4 - 1,即 fib1(n) = 2^(n-1) - 1 = 0.5 * 2^n - 1,所以 fib1(n) 的复杂度为 O(2^n)。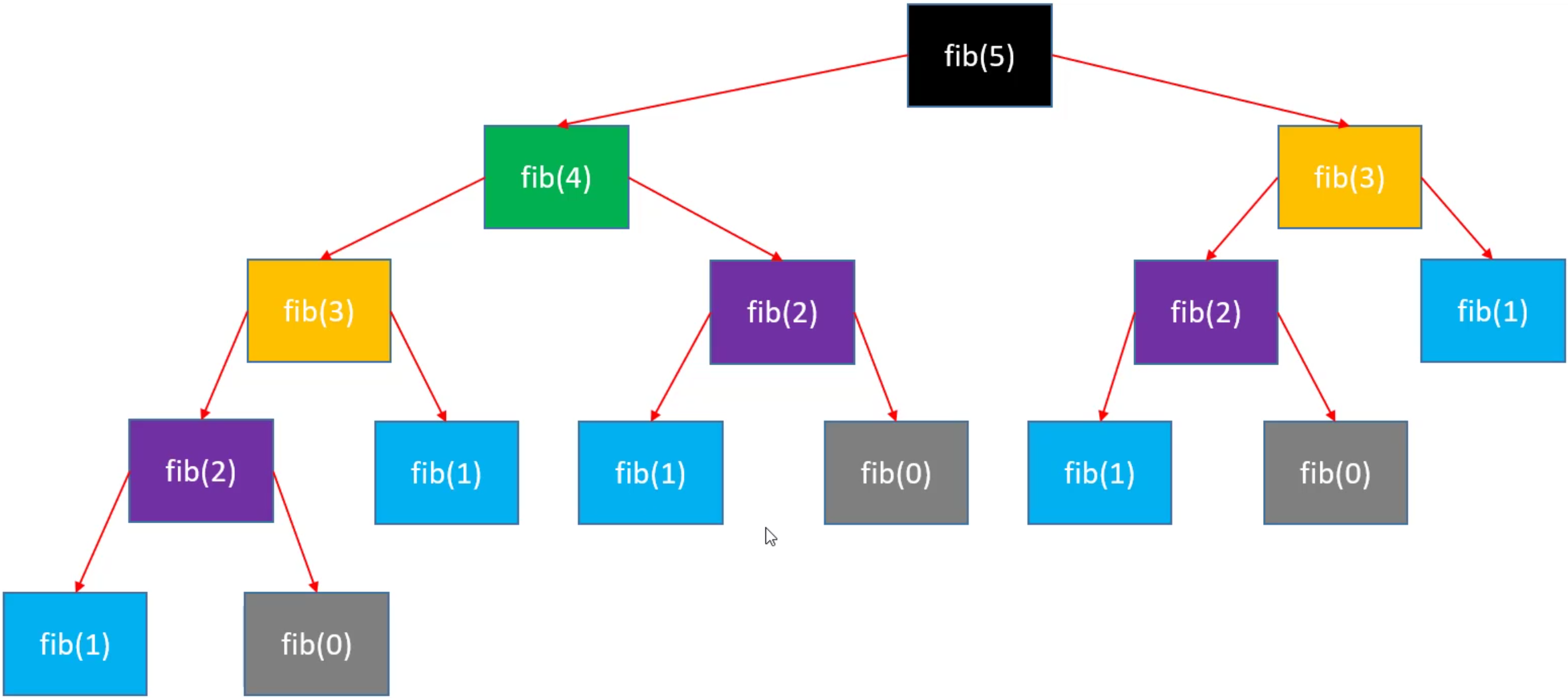
使用函数图像绘制工具绘制 n,2^n: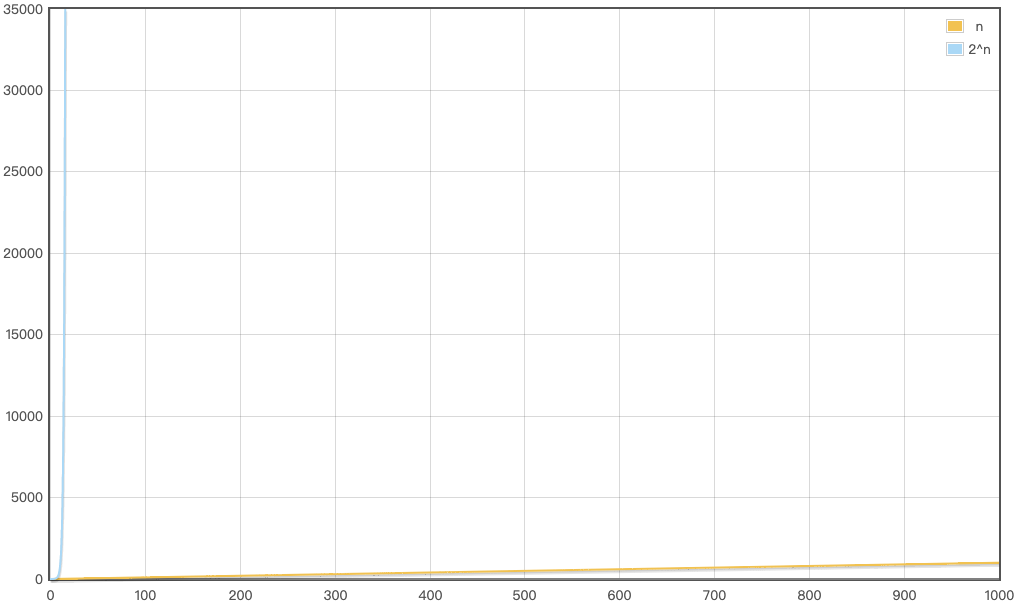
可以看出 fib1(n) 和 fib2(n) 的差别很大,如果有一台1GHz的普通计算机,运算速度为10^9次每秒,让 n = 64,那么:
O(n)大约耗时6.4 * 10^-8秒
O(2^n)大约耗时584.94年
fib2 补充一:
fib2 补充二:使用斐波那契公式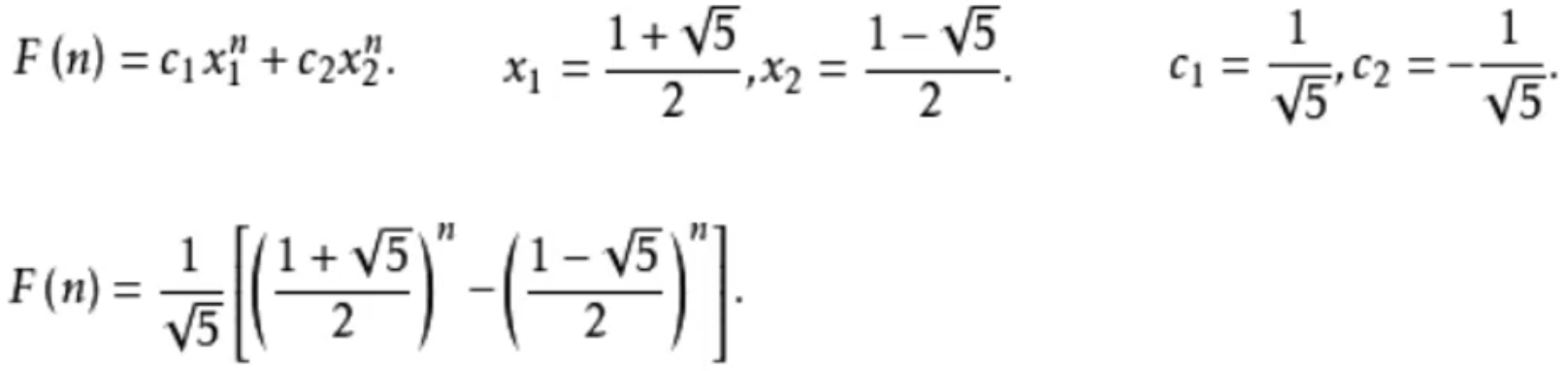
👉 注意:这里是假定 sqrt 和 pow 的时间复杂度都是 O(1) 的前提下,得出 fib3 的时间复杂度是 O(1)。实际情况还得根据使用的 sqrt 和 pow 的真实时间复杂度而定,比如有些 pow 实现的真实复杂度是 O(logn)。
算法的优化方向
- 用尽量稍等存储空间
- 用尽量少的执行步骤
- 空间换时间
- 时间换空间