二叉树(Binary tree)是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个结点最多只能有两棵子树,且有左右之分。
树形结构
二叉树: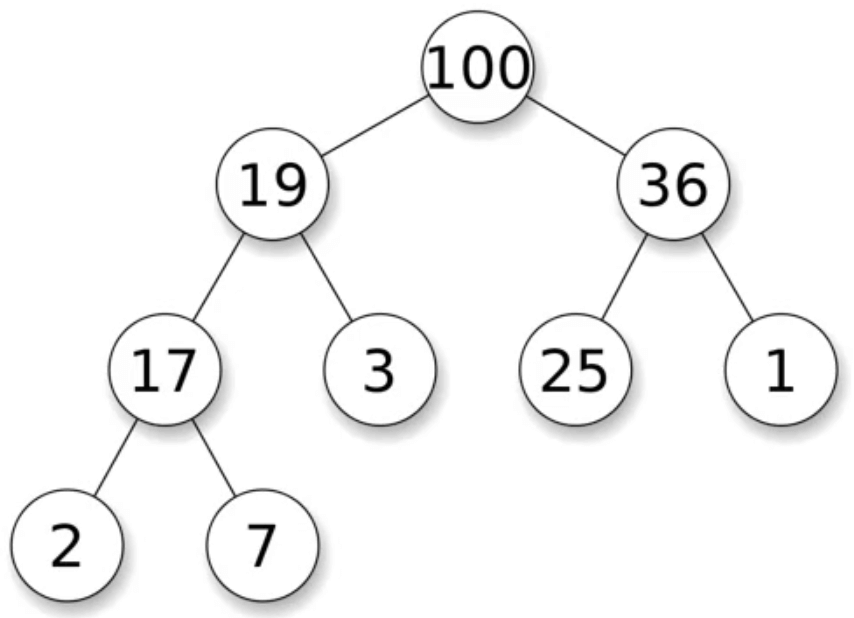
多叉树: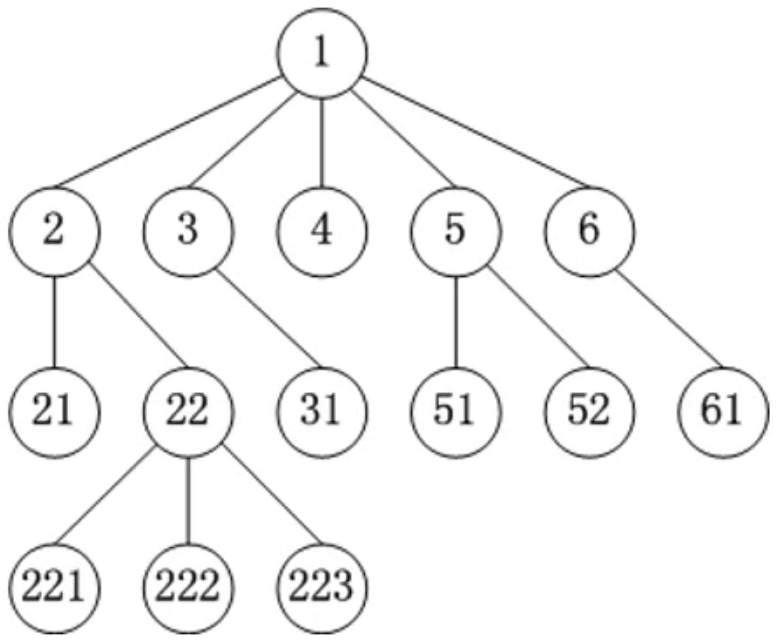
树的基本概念
- 节点
每一个数字都代表一个节点。 - 根节点
1是整棵数的根节点,一棵树只有一个根节点。 - 父节点
1是2、3、4、5、6的父节点,2是21、22的父节点,3是31的父节点,5是51、52的父节点,6是61的父节点,22是221、222、223的父节点。 - 子节点
2、3、4、5、6是1的子节点,21、22是2的子节点,31是3的子节点,51、52是5的子节点,61是6的子节点,221、222、223是22的子节点。 兄弟节点
同一个父节点下的子节点互为兄弟节点,如2、3、4、5、6互为兄弟节点,21、22互为兄弟节点,51、52互为兄弟节点,221、222、223互为兄弟节点。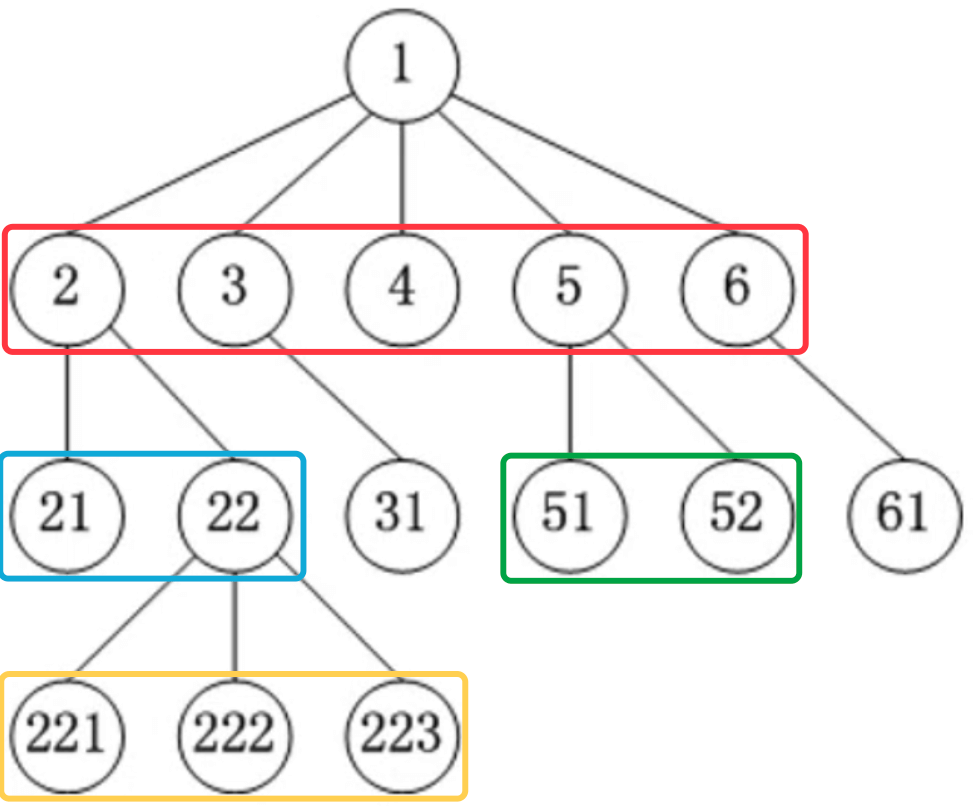
空树
一课树可以没有任何节点,称为空树(一课树可以只有1个节点,也就是只有根节点)。- 子树
2、21、22、221、222、223与3、31与4与5、51、52与6、61都是1的子树。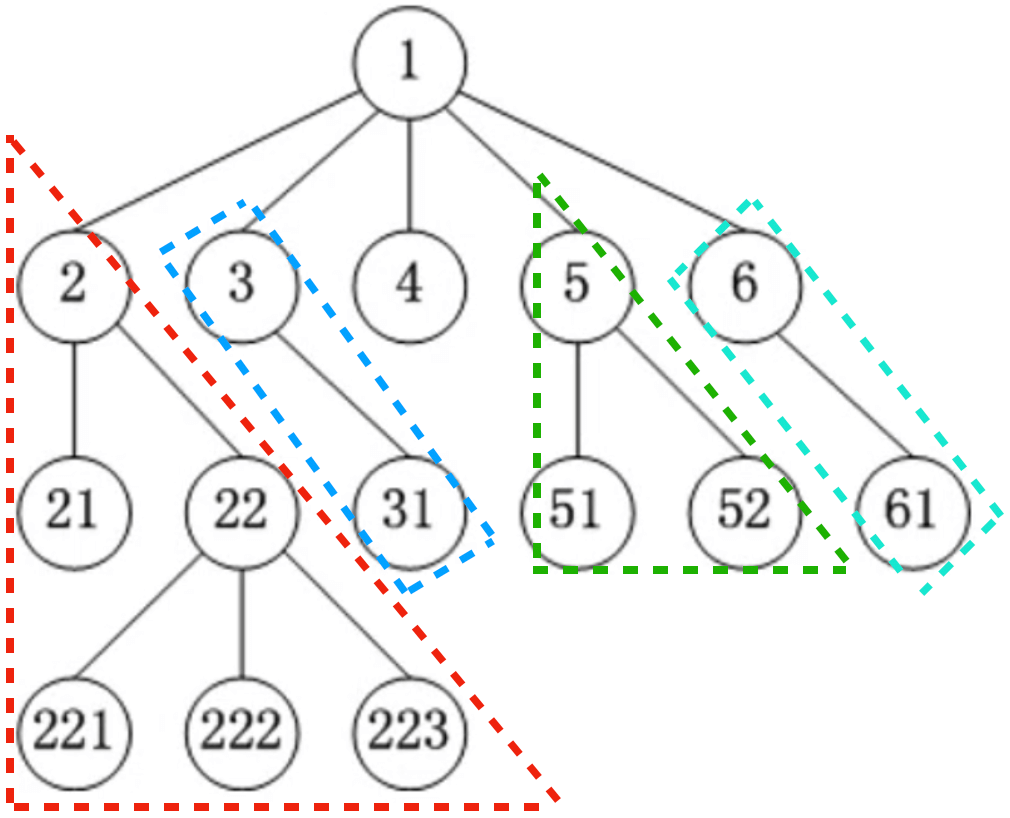
- 左子树
21称为2的左子树。 右子树
22、221、222、223称为2的右子树。节点的度(degree)
即子树的个数,如1的度等于 5,2的度等于 2,3的度等于 1,4的度等于 0,5的度等于 2,6的度等于 1,22的度等于 3。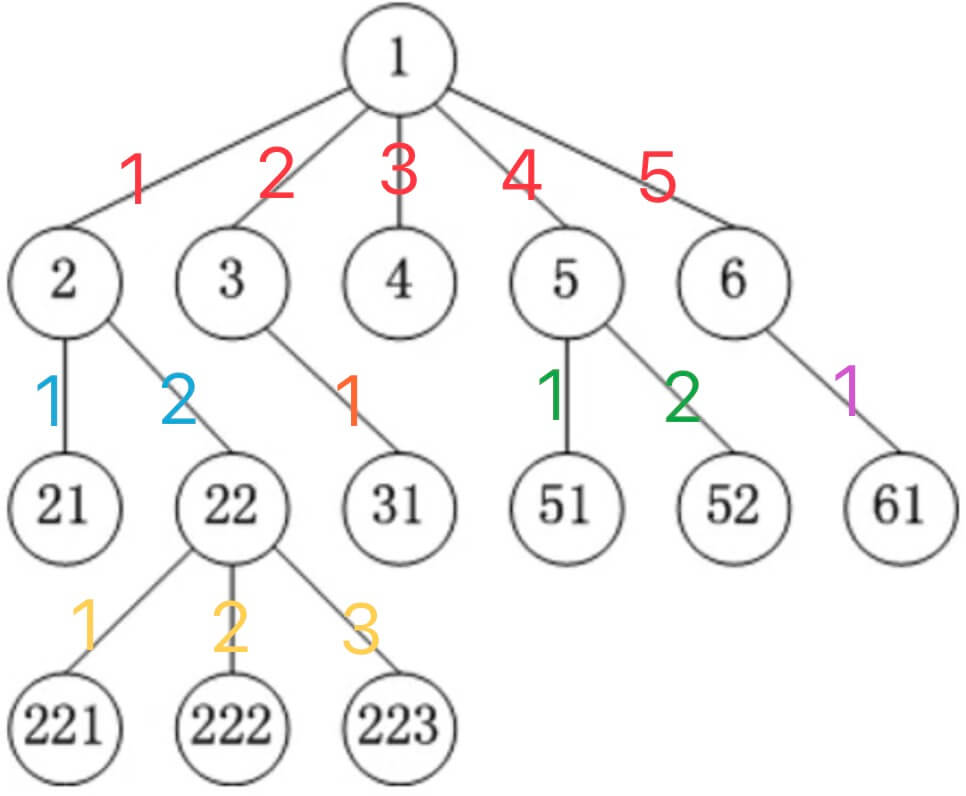
- 树的度
所有节点度中的最大值,如上面这棵多叉树的度就是1的度,等于 5。 - 叶子节点(leaf)
度为 0 的节点,如21、221、222、223、31、4、51、52、61都是叶子节点。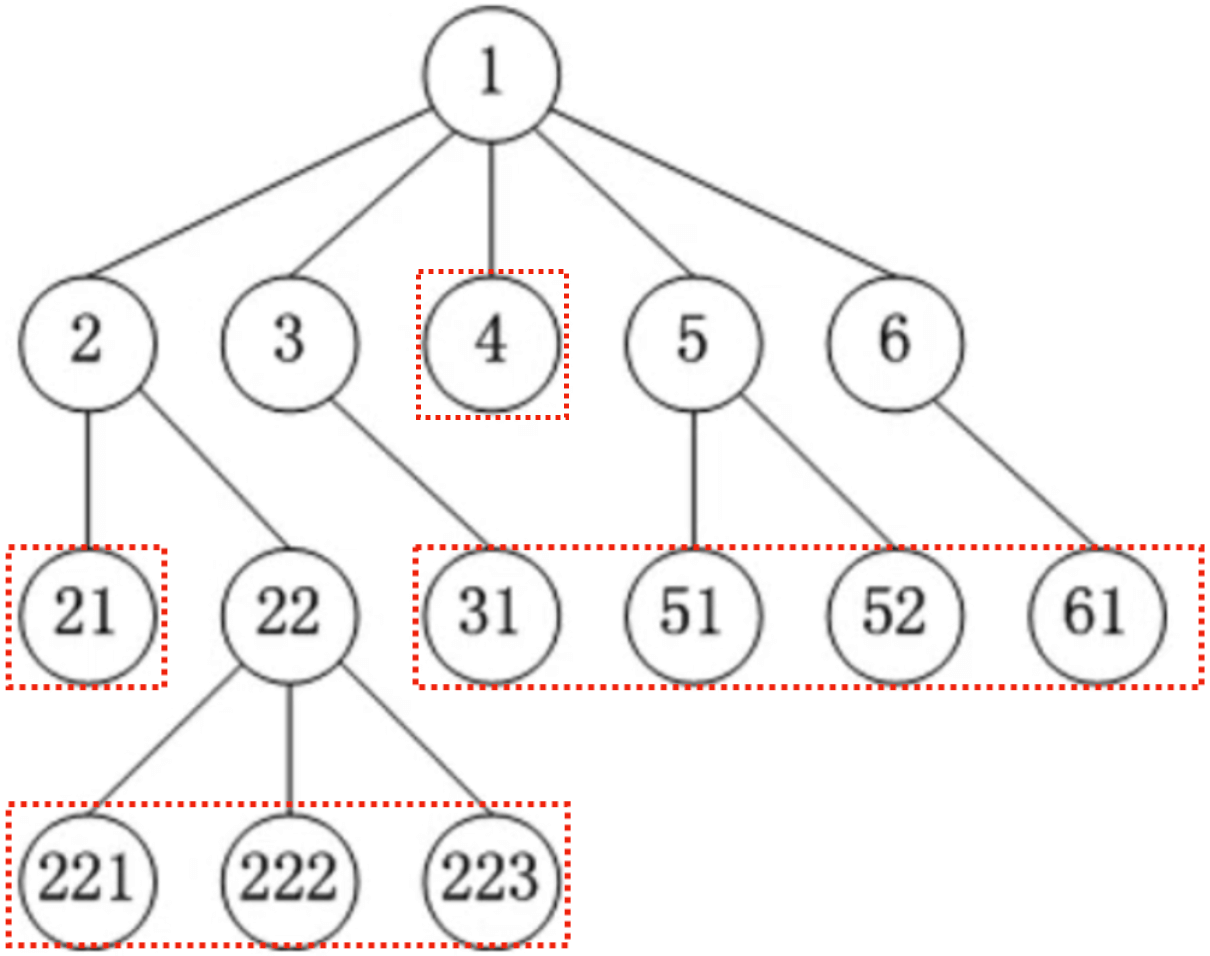
非叶子节点
度不为 0 的节点。层数(level)
根节点在第 1 层,根节点的子节点在第 2 层,以此类推221在第四层(有些教程也从第 0 层开始计算)。- 节点的深度(depth)
从根节点到当前节点的唯一路径上的节点总数,2的深度等于 2,31的深度等于 3。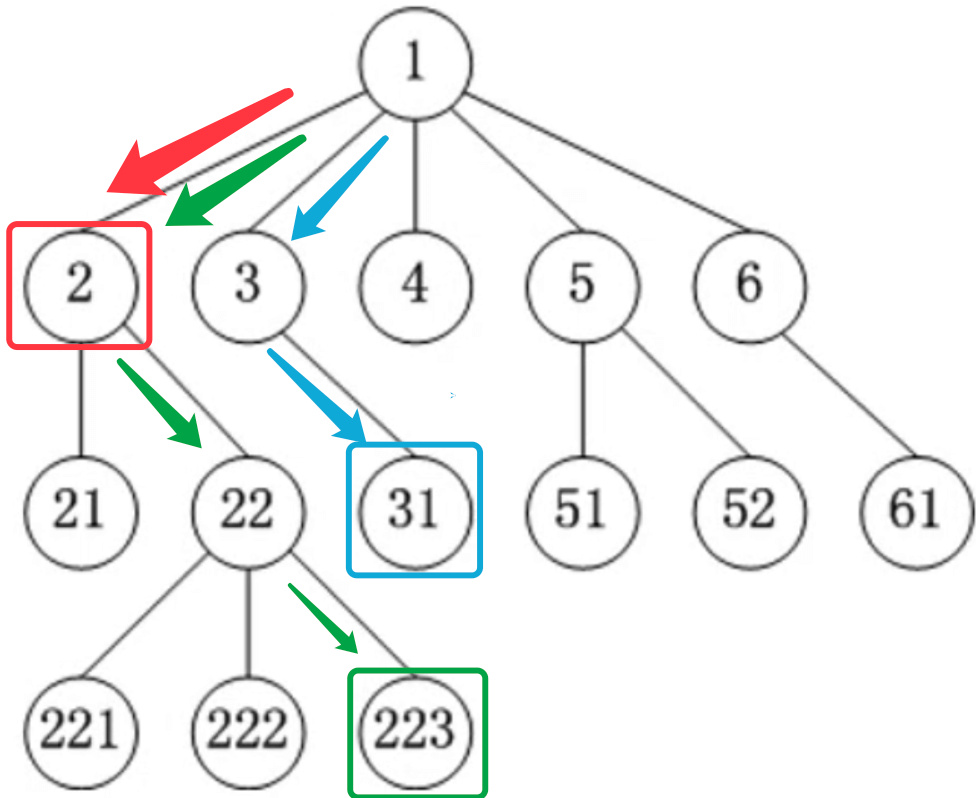
- 节点的高度(height)
从当前节点到最远叶子节点的路径上的节点总数,2的高度等于 3,31的深度等于 0。 - 树的深度
所有节点深度中的最大值,这个树的深度就是221、222、223的深度,等于 4。 - 树的高度
所有节点高度中的最大值,这棵树的高度就是1的高度,等于 4。树的深度等于树的高度。
有序树、无序树、森林
- 有序树
树中的任意节点的子节点之间有顺序关系,如2、3、4、5、6按照大小关系从左至右排。 - 无序树
树中任意节点的子节点之间没有顺序关系,也成为“自由树”。 - 森林
由m(m >= 0)棵互不相交的树组成的集合。
二叉树
二叉树是有序树,二叉树的特点有:
- 每个节点的度最大为 2(最多拥有 2 棵子树,所以所有节点的度要么为 2,要么为 1,要么为 0);
- 左子树和右子树是有顺序的,即使某节点只有一棵子树,也要区分左右子树(
49在左,56在右;96在右)。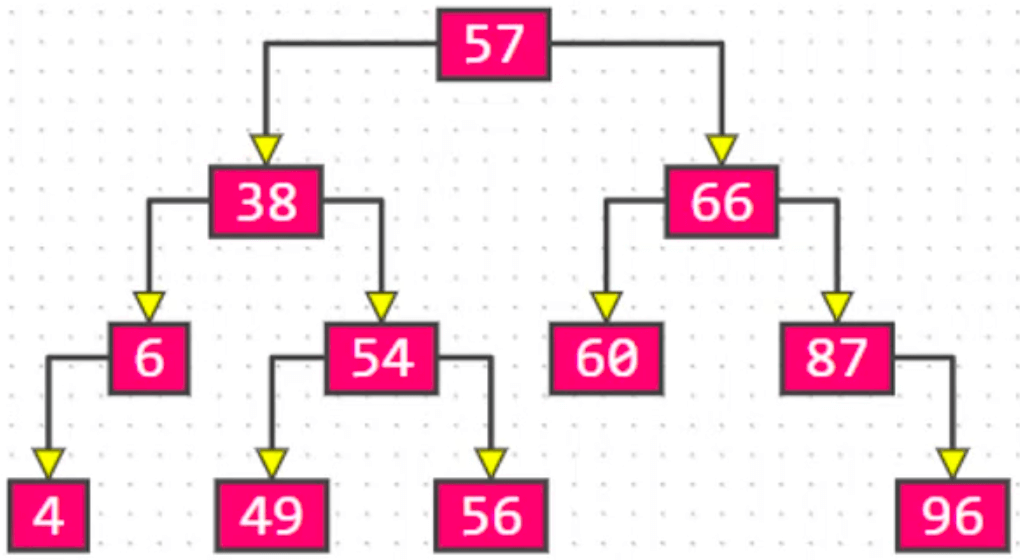
各种情况: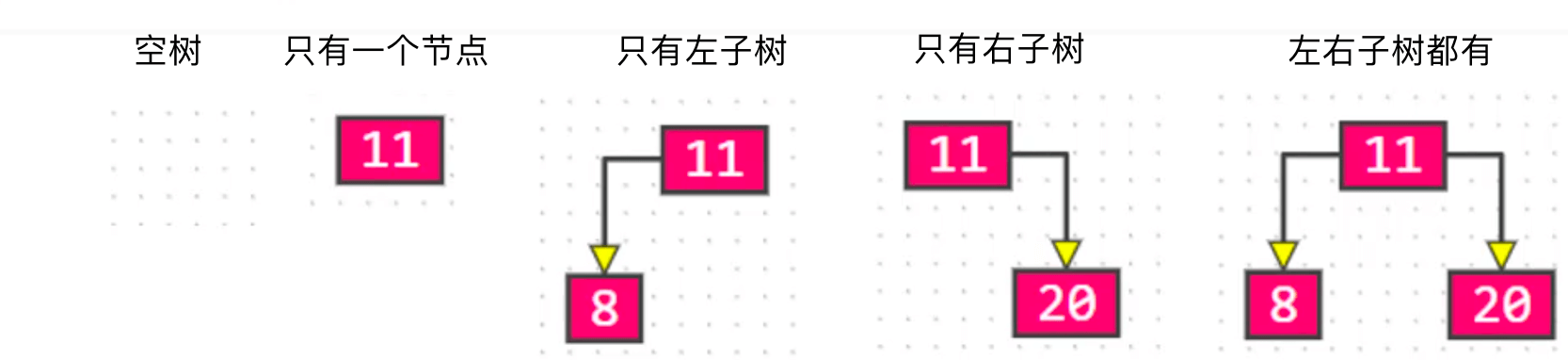
只有左子树或者只有右子树的二叉树,从结构上看跟链表相似: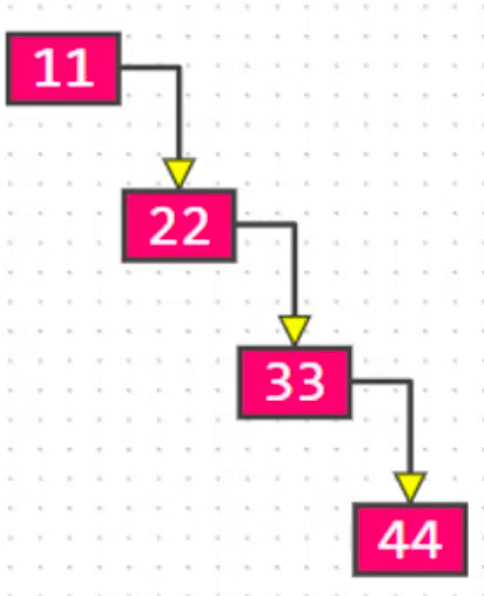
二叉树的性质
- 非空二叉树的第
i层,最多有2^(i-1)个节点(i >= 1); - 在高度为
h的二叉树上最多有2^h - 1个节点(h >= 1); - 对于任何一棵非空二叉树,如果叶子节点个数为
n0,度为 2 的节点个数为n2,则有:n0 = n2 + 1;
假设度为1的节点个数为n1,那么二叉树的节点总数n = n0 + n1 + n2,
二叉树的边数T = n1 + 2 * n2 = n - 1 = n0 + n1 + n2 - 1,
因此n0 = n2 + 1。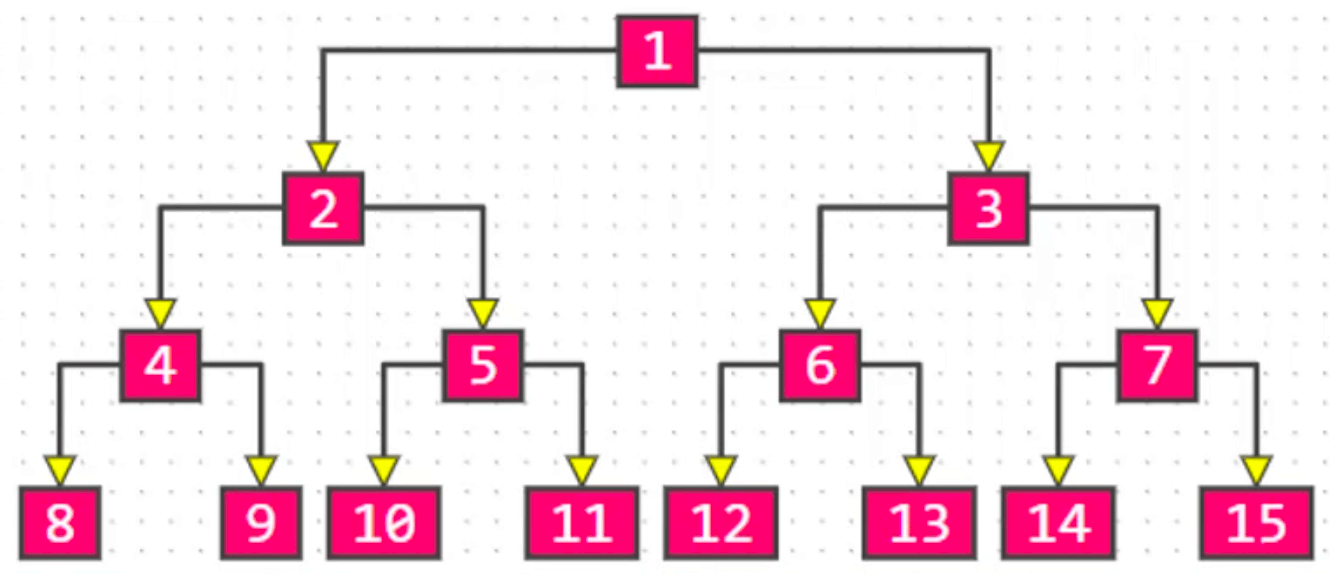
真二叉树
真二叉树:所有的节点的度都要么为 0,要么为 2。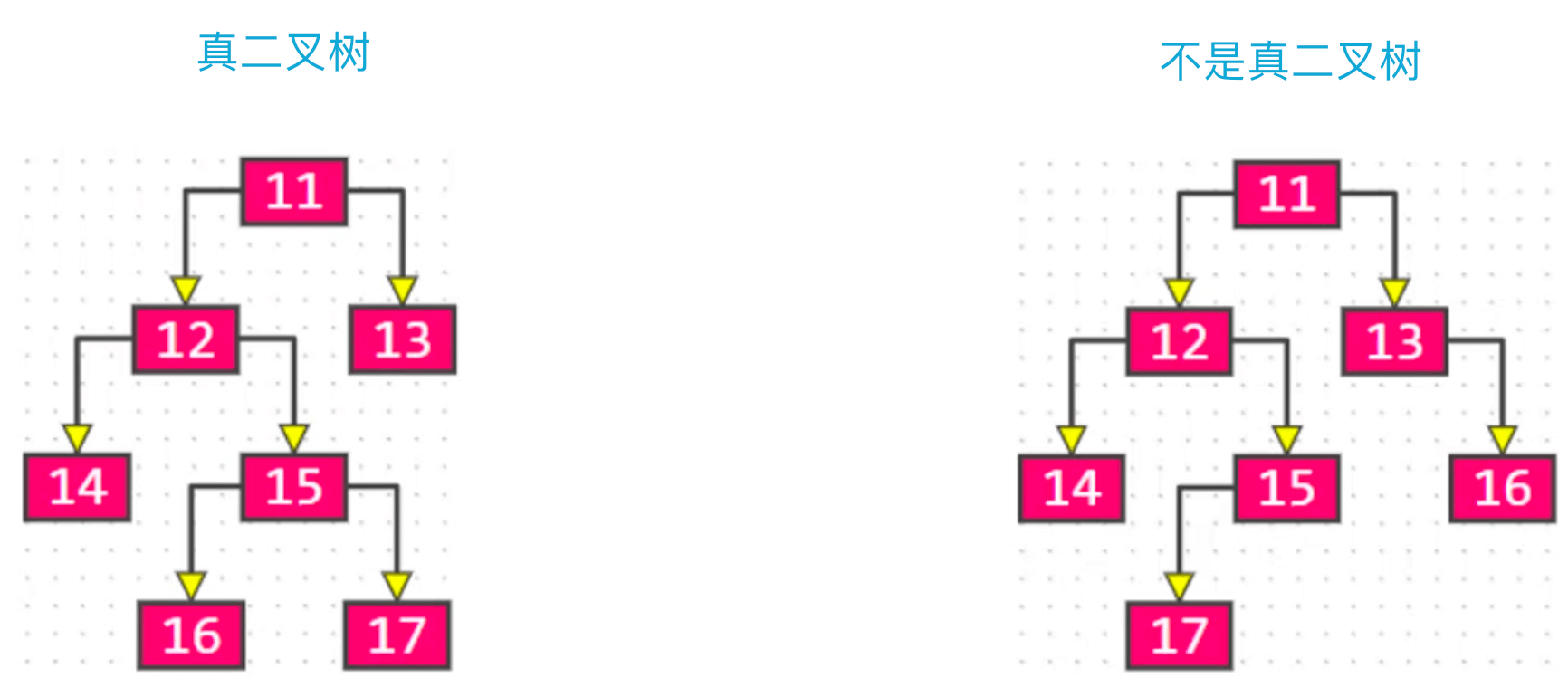
满二叉树
- 满二叉树:最后一层节点的度为 0,其它节点度都为 2。
- 在同样高度的二叉树中,满二叉树的叶子节点数量最多,总节点数量最多。
- 满二叉树一定是真二叉树,真二叉树不一定是满二叉树。
- 假设满二叉树的高度为
h(h >= 1),那么
第i层的节点数量:2^(i-1);
叶子节点数量:2^(h-1);
总结点数量n = 2^h - 1 = 2^0 + 2^1 + 2^2 + ... + 2^(h-1);
高度h = log(2)(n+1);
完全二叉树
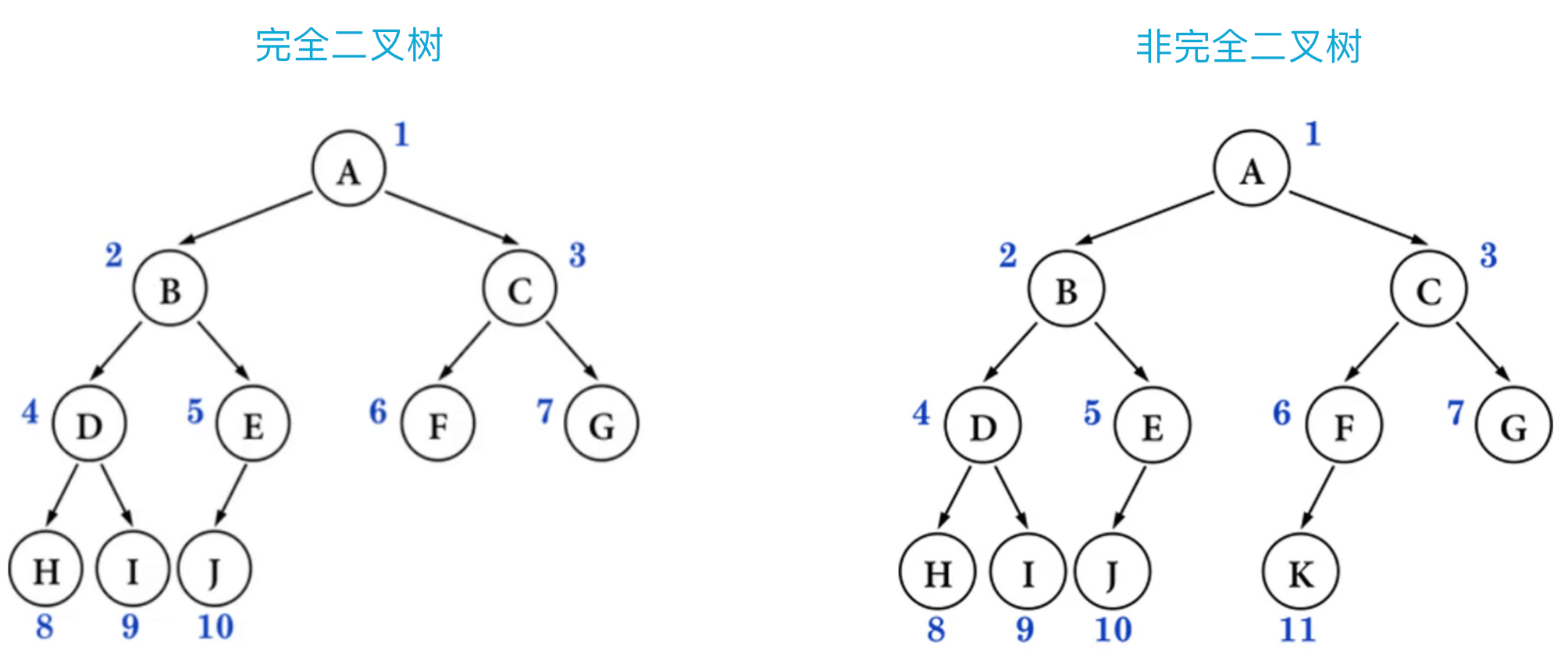
完全二叉树:对节点从上至下、左至右开始编号,其所有编号都能与相同高度的满二叉树中的编号对应。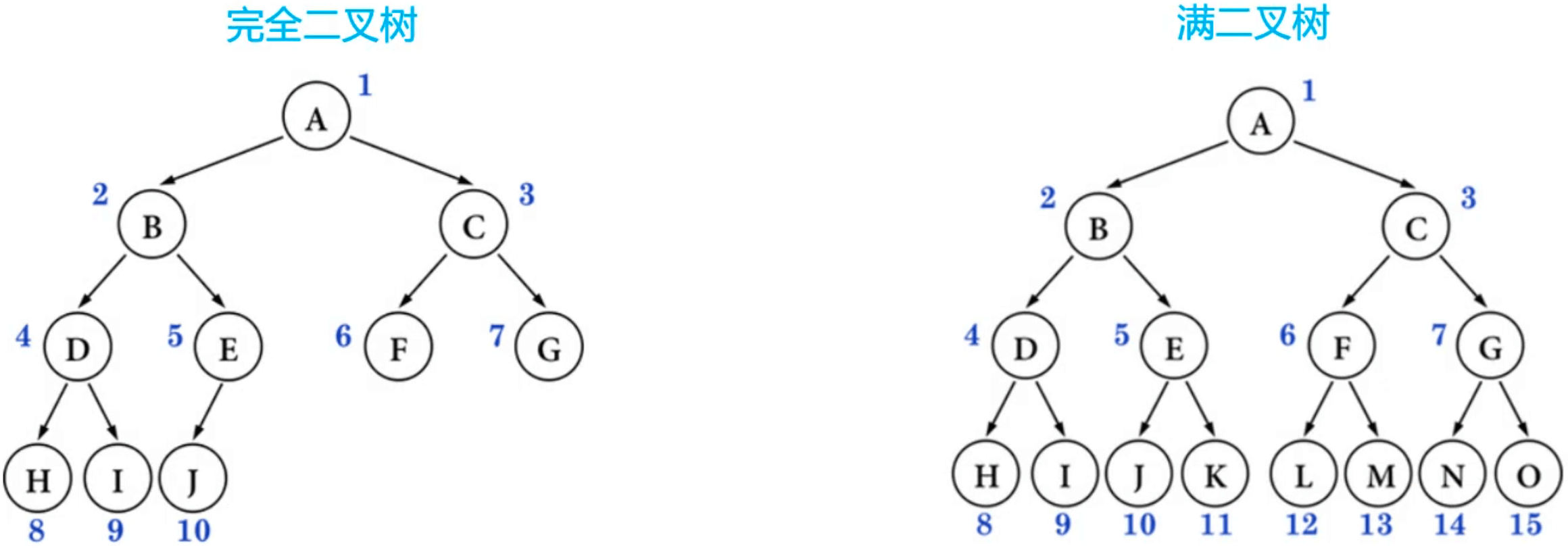
叶子节点只会出现在最后两层,最后一层的叶子节点都是靠左对齐。
完全二叉树从根节点至倒数第二层是一棵满二叉树。
满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。
完全二叉树的性质
- 度为 1 的节点只有左子树。
- 度为 1 的节点要么是 1 个,要么是 0 个。
- 同样节点数量的二叉树,完全二叉树的高度最小。
- 假设完全二叉树的高度为
h(h >= 1),那么
至少有2^(h-1)个节点(2^0 + 2^1 + 2^2 + ... + 2^(h-2) + 1);
最多有2^h - 1个节点(2^0 + 2^1 + 2^2 + ... + 2^(h-2),即满二叉树); - 假设总结点数量为
n,那么2^(h-1) <= n < 2^h->h - 1 <= log(2)(n) < h->h = floor(log(2)(n)) + 1; - 一棵有
n个节点的完全二叉树(n > 0),从上到下、从左到右对节点从 1 开始进行编号,对任意第i个节点:
如果i = 1,它是根节点;
如果i > 1,它的父节点编号为floor(i/2);
如果2i <= n,它的左子节点编号为2i;
如果2i > n,它无左子节点;
如果2i + 1 <= n,它的右子节点编号为2i + 1;
如果2i + 1 > n,它无右子节点;
ps:floor 是向下取整;另外,ceiling 是向上取整;编程中的 *、/ 都是向下取整。
练习
如果一个完全二叉树有 768 个节点,求叶子节点的个数?
叶子节点个数为 768/2 = 389。
解析:
设叶子节点个数为 n0,度为 1 的节点个数为 n1,度为 2 的节点个数为 n2,
则总结点个数 n = n0 + n1 + n2,
又 n0 = n2 + 1,所以 n = 2 * n0 + n1 - 1。
因为完全二叉树的度为 1 的节点个数 n1 要么等于 0,要么等于 1,则
当 n1 == 1 时,n = 2 * n0,n 必然是偶数,所以叶子节点个数 n0 = n/2,非叶子节点个数 n1 + n2 = n/2;
当 n1 == 0 时,n = 2 * n0 - 1,n 必然是奇数,所有叶子节点个数 n0 = (n + 1)/2,非叶子节点个数 n1 + n2 = (n - 1)/2。
(n0 = (n + 1)/2 可以写作 n0 = n/2 + 1/2,结合 n1 == 1 的情况(n0 = n/2),叶子节点个数可以总结为👇)
综上,叶子节点个数 n0 = floor((n + 1)/2) = ceiling(n/2),非叶子节点个数 n1 + n2 = floor(n/2) = ceiling((n-1)/2)。