运算符

发表于

赋值和算术运算符

基本概念

  • 一元运算符，对一个目标进行操作。一元前缀运算符：!b，一元后缀运算符：b!。

  • 二元运算符，对两个目标进行操作。如a + b，同时因为它们出现在两个目标之间，所以是中缀运算符。

  • 三元运算符，对三个目标进行操作。Swift 语言仅有一个三元运算符，即三元条件运算符 a ? b : c。

Swift 支持 C 中大多数的标准运算符，同时也增加了一些能力，用来排除常见代码错误：

  1. 赋值符号（=）不会返回值，以防止它和等于符号（==）产生误用。
  2. 算数符号（+，-，*，/，%等）可以检测并阻止值溢出，如存储类型放入大于允许范围的数字。

赋值运算符

  • =：赋值运算符，将一个值赋值给另外一个值。如果赋值符号右侧是拥有多个值的元组，则元组的元素将会一次性拆分成常量和变量。

赋值运算符不会返回值

在 OC 中，赋值运算符在赋值成功后会返回 true：

01

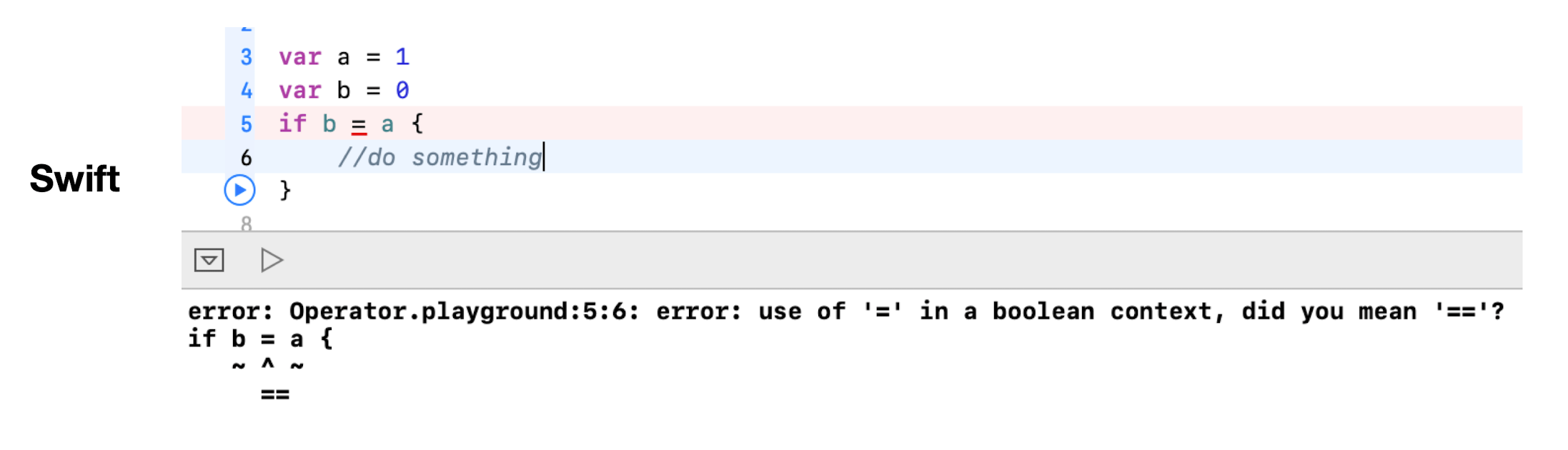
而 Swift 的赋值符号自身不会返回值：

02

算术运算符

标准运算符

+、-、*、/ 是标准算术运算符。

加法运算符也支持 String 的拼接：

1
let str = str1 + str2
  • Swift 算术运算符默认不允许值溢出

余数运算符

1
let c = a % b

余数：指整数除法中被除数未被除尽部分，且余数的取值范围为0到除数之间（不包括除数）的整数。
03

除数为负数时，也是用同样的方法进行计算：

1
2
3
let c = -4 % 3
print(c)
// Prints -1

被除数为负数时，负号会被忽略：

1
2
3
let c = 4 % -3
print(c)
// Prints 1

一元

  • 一元减号运算符（-）：直接放置在操作的值前边。数字值的正负号可以用前缀 - 来切换。
  • 一元加号运算符（+）：直接返回操作的值，不会对其进行任何的修改。

溢出运算符

向一个整数赋值超过它容量的值时，Swift 会报错，而不是生成一个无效的数。

  • &+ 溢出加法
  • &- 溢出减法
  • &* 溢出乘法

值溢出

无符号整型数值和有符号整型数值都可以向上溢出或向下溢出。

当发生上溢时，它们会从数值所能容纳的最大数变成最小数。

当发生下溢时，它们会从数值所能容纳的最小数变成最大数。

无符号整型数值，向上溢出：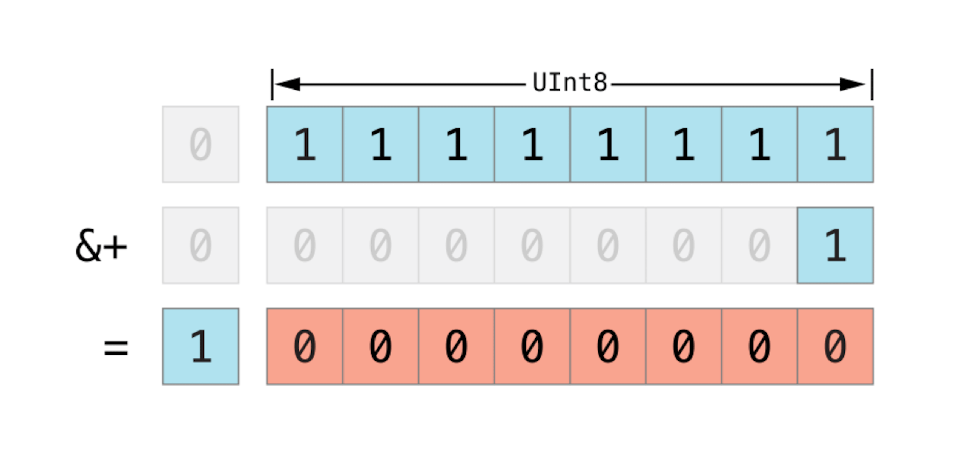
04

无符号整型数值，向下溢出：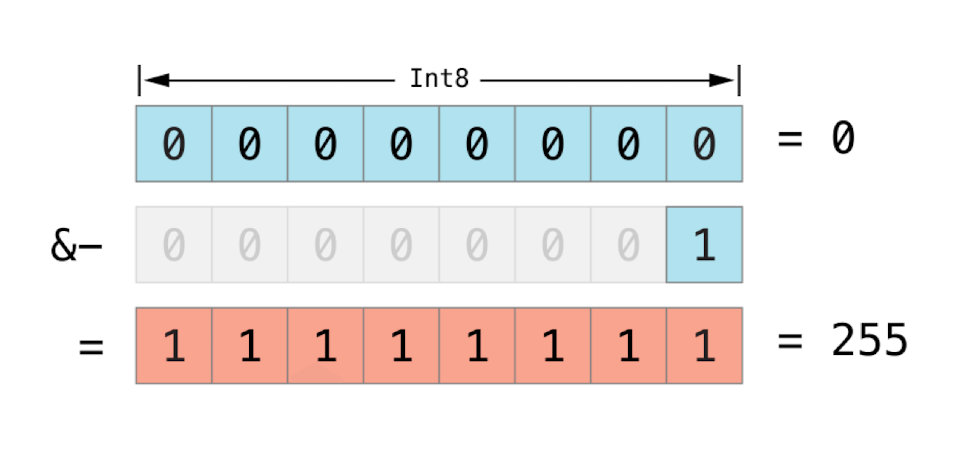
05

有符号整型数值，向下溢出：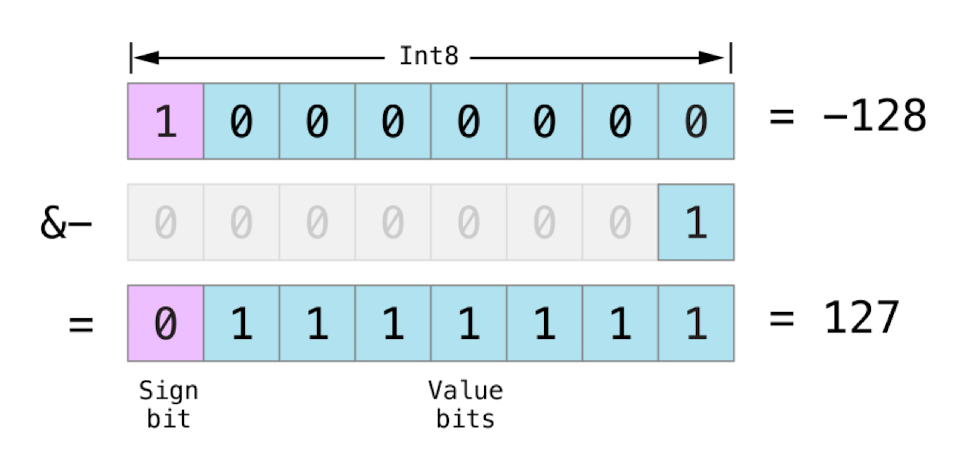
06

Swift 算术运算符默认不允许值溢出：
07

可以使用溢出加法&+：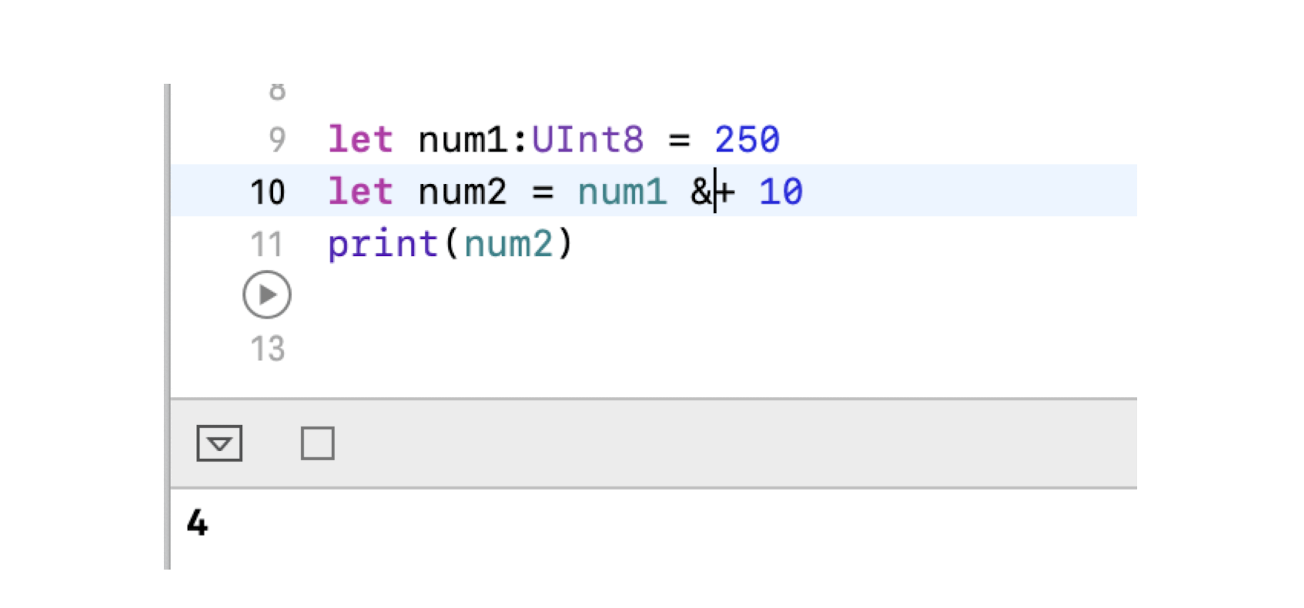
08

合并空值运算符

如果 a 有值则返回 a，不会再判断 b；如果 a 没有值（nil），则返回默认值 b：

1
let c = a ?? b

其中，a 必须是一个可选类型，b 必须与 a 的储存类型相同。

合并空值运算符就是三元运算符，是三元运算符作用到 Optional 上的缩写版：

1
2
3
4
5
// 合并空值运算符
let c = a ?? b
// 三元运算符
let c = a != nil ? a! : b

应用效果对比

1、使用强制解包，有崩溃风险，如果 num1 或 num2 为 nil 会崩：

1
2
3
func addTowNumber(num1: Int?, num2: Int?) -> Int {
    return num1! + num2!
}

2、使用 if 判断，代码量比较多：

1
2
3
4
5
6
7
func addTowNumber(num1: Int?, num2: Int?) -> Int {
    if num1 != nil && num2 != nil {
        return num1! + num2!
    } else {
        return 0
    }
}

3、使用合并控制运算符 ??

1
2
3
func addTowNumber(num1: Int?, num2: Int?) -> Int {
    return (num1 ?? 0) + (num2 ?? 0)
}

区间运算符

闭区间运算符

a...b：闭区间运算符，定义了从 a 到 b 的一组范围，包含 a 和 b。a 的值不能大于 b。

1
2
3
4
5
6
7
8
for index in 1...5 {
    print(index)
}
// 1
// 2
// 3
// 4
// 5

半开区间运算符

a..<b：半开区间运算符，定义了从 a 到 b 的一组范围，包含 a 不包含 b。a 不能大于 b，如果 a 与 b 相等，则返回空。

1
2
3
4
5
6
7
for index in 1..<5 {
    print(index)
}
// 1
// 2
// 3
// 4

单侧区间

单侧区间是闭区间的另外一种形式，让区间朝一个方向尽可能的远。

  • a...：区间左边大于等于 a。
  • ...b：区间右边小于等于 b。

半开区间运算符也有单侧形式：

  • ..<b：区间右边小于b。

举例1：从索引2到数组最后一个元素

1
2
3
4
5
6
let names = ["zhangsan", "lisi", "wangwu", "zhaoliu"]
for name in names[2...] {
    print(name)
}
// wangwu
// zhaoliu

举例2：从数组第一个元素开始到索引2：

1
2
3
4
5
6
7
let names = ["zhangsan", "lisi", "wangwu", "zhaoliu"]
for name in names[...2] {
    print(name)
}
// zhangsan
// lisi
// wangwu

举例3：从数组第一个元素开始到索引2前一个元素：

1
2
3
4
5
6
let names = ["zhangsan", "lisi", "wangwu", "zhaoliu"]
for name in names[..<2] {
    print(name)
}
// zhangsan
// lisi

举例4：单侧区间不仅用于下标，还可以在上下文中使用

1
2
3
4
5
6
7
let range = ...5
print(range.contains(7))
print(range.contains(4))
print(range.contains(-1))
// false
// true
// true

字符串索引区间

区间运算符在字符串中的应用：删除指定范围的字符

1
2
3
4
5
var welcome = "hello,world"
let range = welcome.index(welcome.endIndex, offsetBy: -6) ..< welcome.endIndex
welcome.removeSubrange(range)
print(welcome)
// Prints "hello"

倒序索引

1
2
3
4
var welcome = "hello,world"
let reversedWelcome = String(welcome.reversed())
print(reversedWelcome)
// Prints "dlrow,olleh"

Comparable 区间

区间运算符作用在 Comparable 类型上，返回闭区间和半闭区间。

1
2
3
4
5
6
7
8
let welcome = "Hello"
let interval = "a"..."z"
for c in welcome {
    if !interval.contains(String(c)) {
        print("\(c)不是小写字母")
    }
}
// Prints "H不是小写字母"

位运算符

位取反运算符

  • ~ 位取反运算符，是对所有位的数字进行取反操作。

09

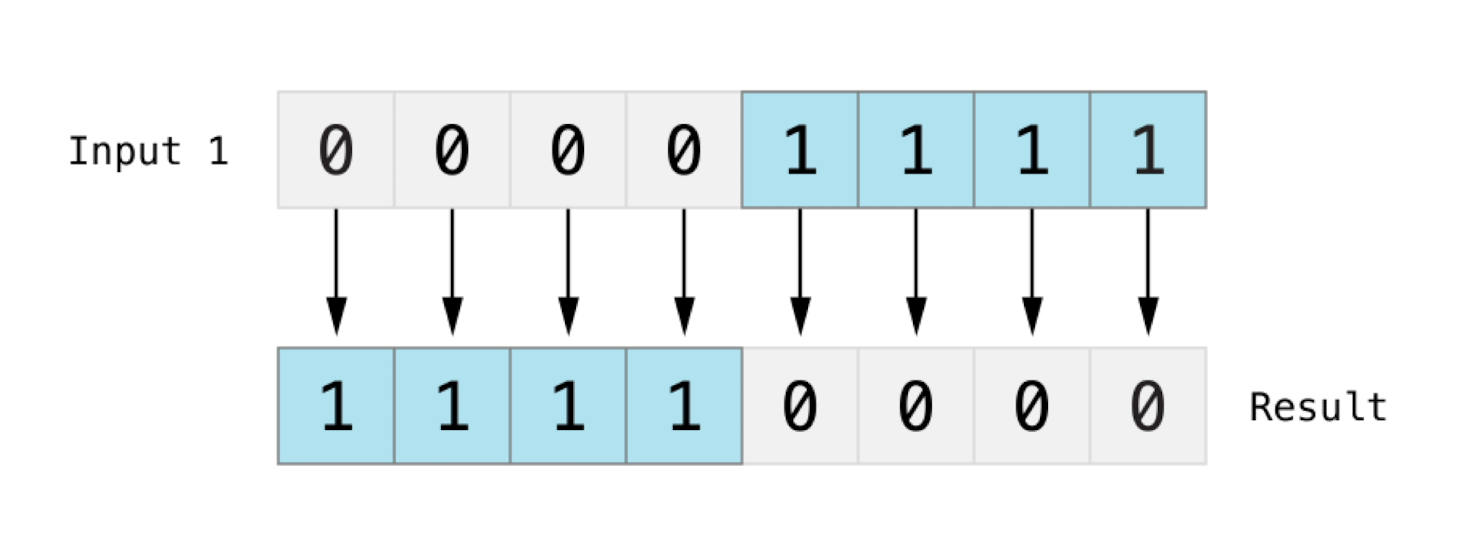
位与运算符

  • & 位与运算符，可以对两个数的比特位进行比较，返回一个新的数，当两个比特位都是 1 时返回 1。

10

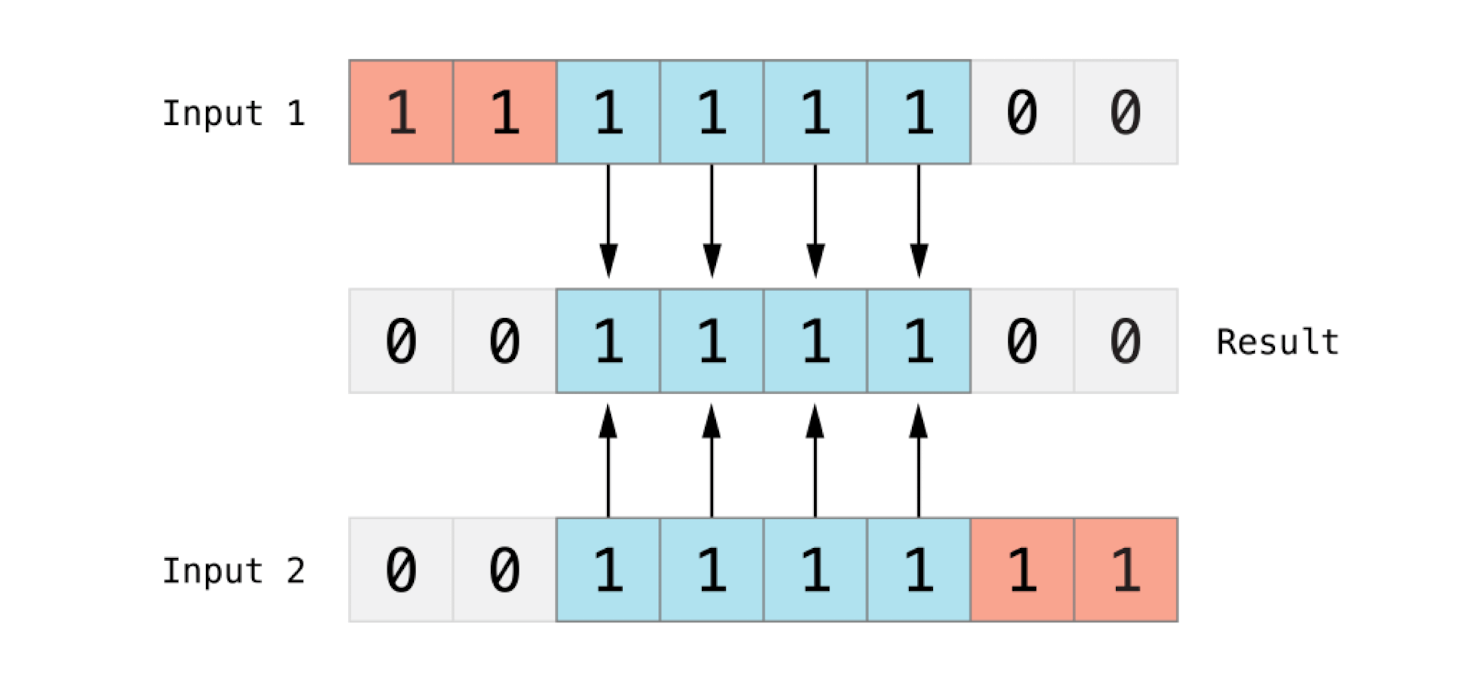
位或运算符

  • | 位或运算符，可以对两个数的比特位进行比较，返回一个新的数，当两个比特位任意一个为 1 时返回 1。

11

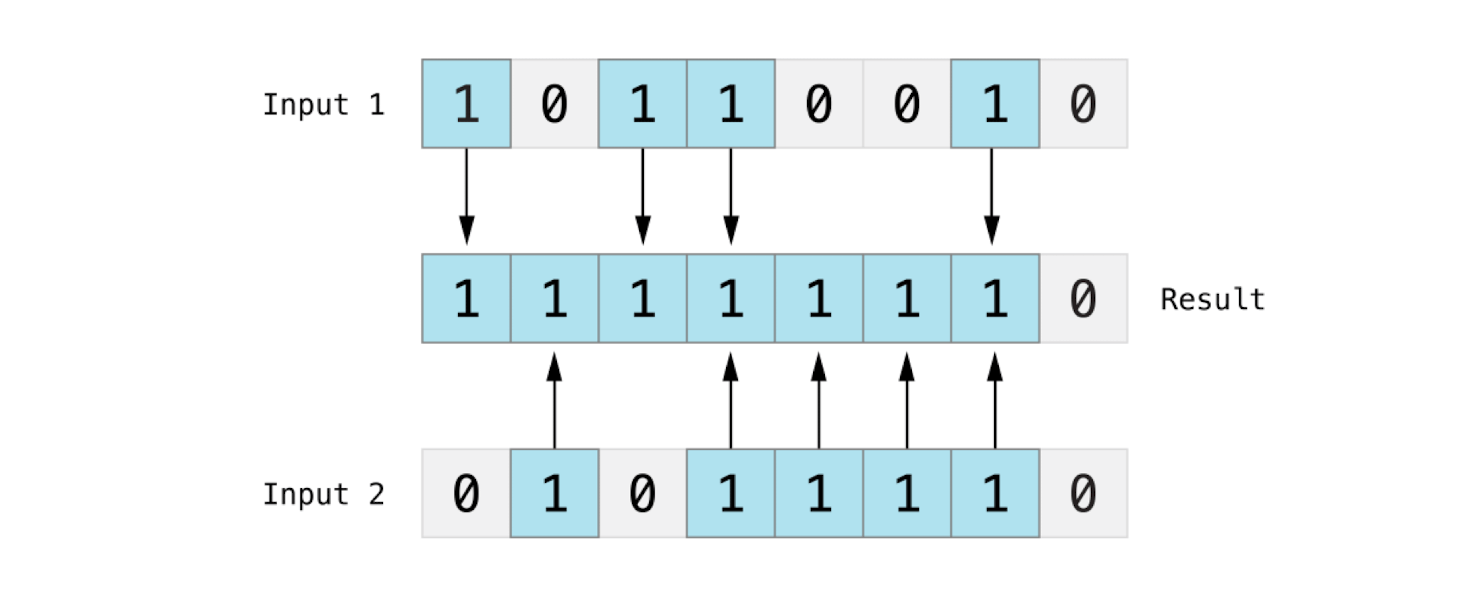
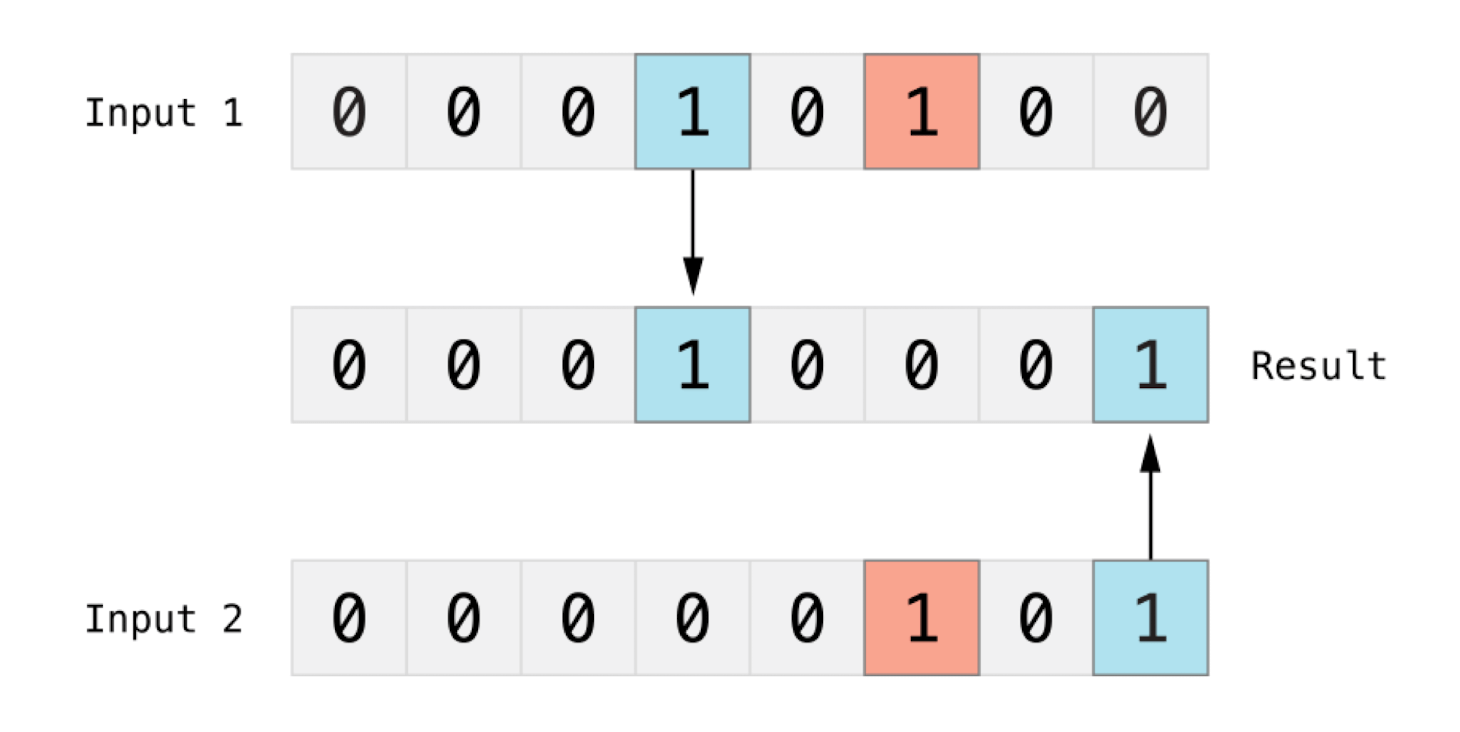
位异或运算符

  • ^ 为异或运算符，或者叫“互斥或”，可以对两个数的比特位进行比较，返回一个新的数，当两个比特位不相同 时返回 1。

12

位左移和右移运算符

  • << 位左移运算符，可以把所有位数的数字向左移动一个确定的位数。
  • >> 位右移运算符，可以把所有位数的数字向右移动一个确定的位数。

位左移和位右移具有将整数乘以或除以二的效果。将一个数左移一位相当于把这个数翻倍，将一个数右移一位相当于把这个数减半。

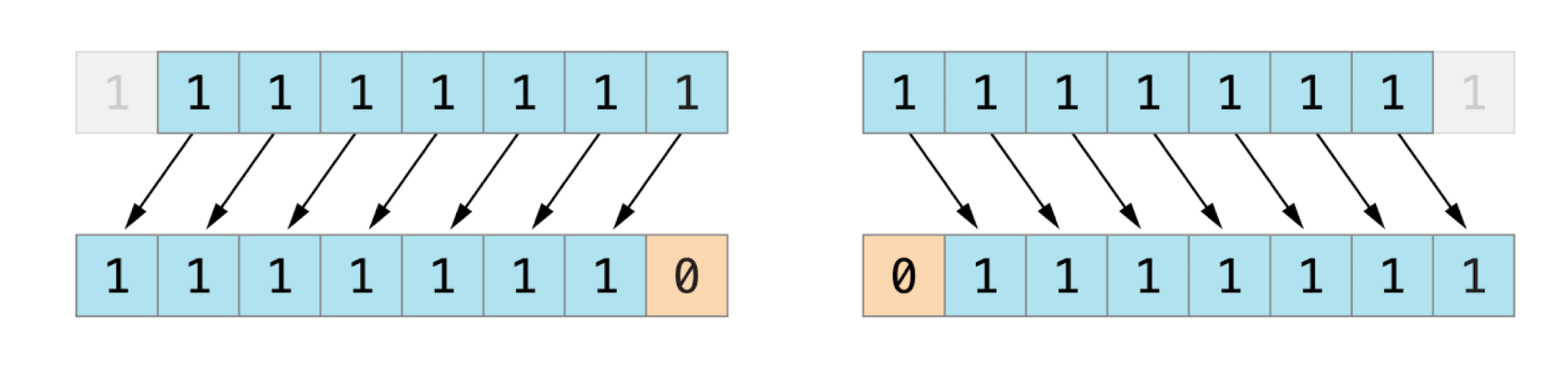
无符号整数的移位操作

实现过程：

  1. 已经存在的比特位按指定的位数进行左移和右移；
  2. 任何移动超出整型存储边界的位都会被丢弃；
  3. 用 0 来填充向左或向右移动后产生的空白位。

13

有符号整数的移位操作

符号位：有符号整数用第一位表示正数还是负数。符号位为 0 表示正数，1 表示负数。

数值位：除第一位外其余的位，存储了实际的值。

有符号正整数和无符号数的存储方式是一样的，都是从 0 开始算起。

14

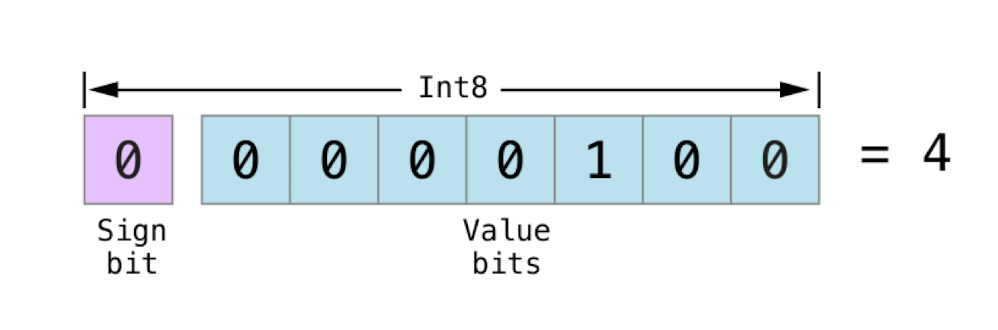
但是负数的存储方式略有不同，它存储的是 2 的 n 次方减去它的绝对值，这里的 n 为数值位的位数。

15

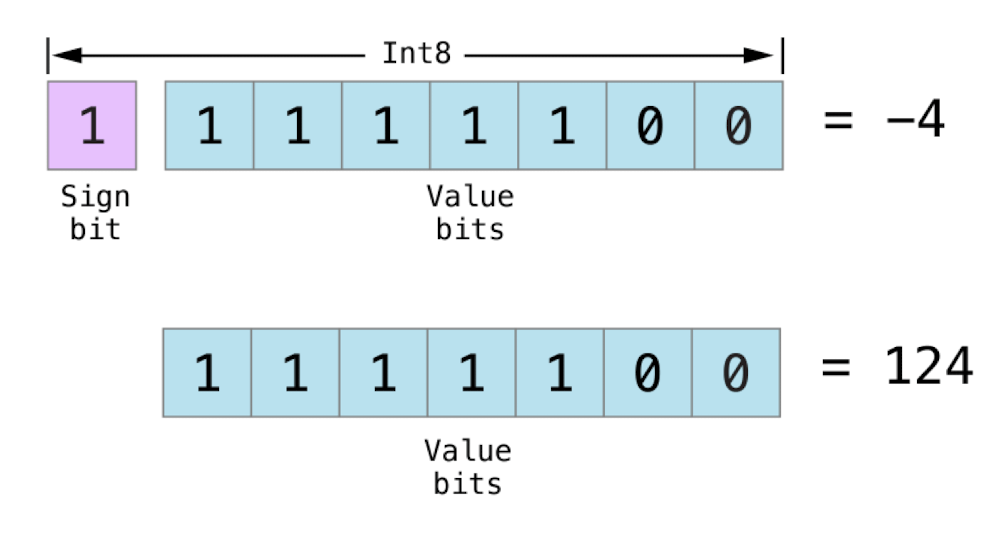
-4 的存储位 128 - 4 = 124。

补码表示的优点

对于算式 -4 + -1，先将两个数的全部八个比特位相加（包括符号位），再将计算结果中超出的部分丢弃。

16

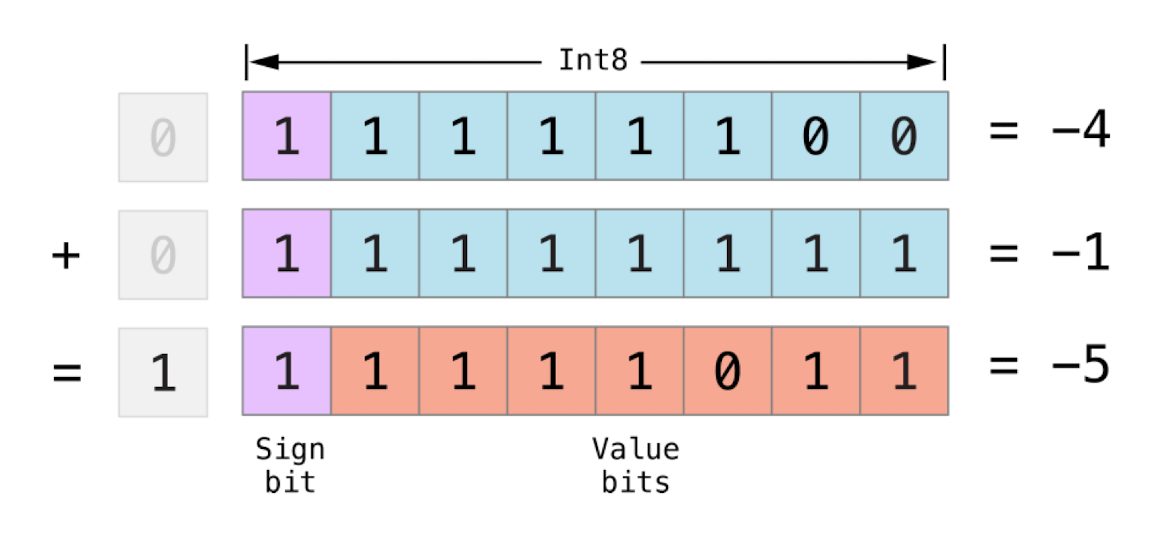
-4 的存储位 2^8 - 4，-1 的存储位 2^8 - 1，-5 的存储位 2^8 - 5。
-4 + -1 = 2^8 - 4 + 2^8 - 1，将计算结果中超出的部分丢弃（去掉一个2^8）。
即 -4 + -1 = 2^8 - 4 - 1 = 2^8 - 5，等于 -5。

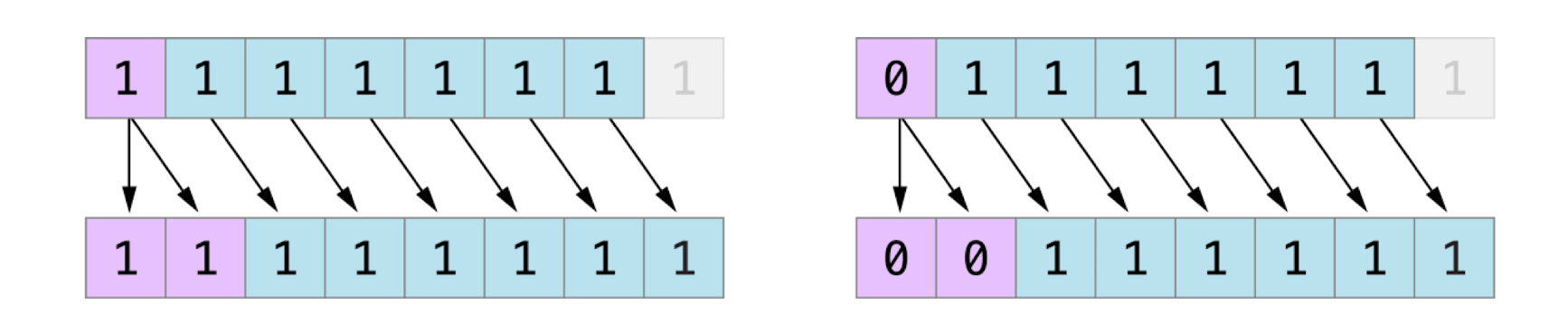
使用二进制补码可以使负数的位左移和右移操作，得到跟正数同样的效果，即每向左移一位就将自身的数值乘以 2，每向右移一位就将自身的数值除以 2。

要达到此目的，对有符号整数的右移有一个额外的规则：当对正整数进行位右移操作时，遵循与无符号整数相同的规则，但是对于移位产生的空白位使用符号位进行填充，而不是 0。

17

位运算符经典算法

两个数字交换

1
2
3
4
5
6
7
8
9
var a = 10
var b = 8
a = a ^ b
b = a ^ b
a = a ^ b
print(a)
print(b)
// 8
// 10

求无符号整数二进制中1的个数

  • 给定一个无符号整型（UInt）变量，求其二进制表示中 “1” 的个数，要求算法的执行效率尽可能的高。

思路：看一个八位整数 10 100 001，先判断最后一位是否为 1，而“与”操作可以达到目的。可以把这个八位的数字与 00 000 001 进行“与”操作。如果结果为1，则表示当前八位数的最后一位为1，否则为0。怎么判断第二位呢？向右移位，在延续前面的判断即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
func countOfOnes(num: UInt) -> UInt {
    var count: UInt = 0
    var temp = num
    while temp != 0 {
        count += temp & 1
        temp = temp >> 1
    }
    return count
}
print(countOfOnes(num: 4))
print(countOfOnes(num: 5))
// Prints 1
// Prints 2

思考：如果整数的二进制中有较多的 0，那么我们每一次右移一位做判断会很浪费，怎么改进呢？有没有办法让算法的复杂度只与“1”的个数有关？

思路：为了简化这个问题，先考虑只有高位有“1”的情况。例如：11 000 000，如何跳过前面低位的 6 个 0，而直接判断第七位的 1？我们可以设计 11 000 000 和 10 111 111（也就是 11 000 000 - 1）做“与”操作，消去最低位的 1。如果得到的结果为 0，说明已经找到（消去）里面最后一个 1。如果不为 0，那么说明消去了最低位的 1，但是二进制中还有其它的 1，计数器加一继续上面的操作。

计数器 count = 0

步骤一：整数不为0，说明二进制里肯定有 1，count = 1

11 000 000 & 10 111 111 = 10 000 000（消去第七位的 1）。

步骤二：结果不为0，说明二进制里还有 1，count = 2

10 000 000 & 01 111 111 = 0（消去第八位的 1）。

步骤三：结果为0，终止，返回 count 为 2。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func countOfOnes(num: UInt) -> UInt {
    var count: UInt = 0
    var temp = num
    while temp != 0 {
        count += 1
        temp = temp & (temp - 1)
    }
    return count
}
print(countOfOnes(num: 4))
print(countOfOnes(num: 5))
// Prints 1
// Prints 2

如何判断一个整数为2的整数次幂

  • 给定一个无符号整型（UInt）变量，判断是否为 2 的整数次幂。

思路：一个整数如果是 2 的整数次方，那么它的二进制表示中有且只有一位是 1，其它所有位都是 0。根据前面的分析，把这个整数减去 1 后再和它自己做“与”运算，这个整数中唯一的 1 就变成 0 了，也就是得到的结尾为 0。

1
2
3
4
5
6
7
8
func isPowerOfTwo(num: UInt) -> Bool {
    return (num & (num - 1)) == 0;
}
print(isPowerOfTwo(num: 4))
print(isPowerOfTwo(num: 5))
// Prints true
// Prints false

缺失的数字

  • 很多成对出现的正整数保存在磁盘文件中，注意成对的数字不一定是相邻的，如 2，3，4，3，4，2……，由于意外有一个数字消失了，如何尽快找到是哪个数字消失了？

思路：考虑“异或”操作的定义，当两个操作数的对应位不同时，该数的对应位就为 1。也就是说如果是 相等的两个数“异或”，得到的结果为 0，而 0 与任何数字“异或”，得到的是那个数字本身。所以可以将所的数字做“异或”操作，因为只有一个数字消失，那么其它两两出现的数字“异或”后为 0，0与仅有的一个数字做“异或”，就得到了消失的数字是哪个。

1
2
3
4
5
6
7
8
9
10
func findLostNum(nums: [UInt]) -> UInt {
    var lostNum: UInt = 0
    for num in nums {
        lostNum = lostNum ^ num
    }
    return lostNum
}
print(findLostNum(nums: [1, 2, 1, 3, 2, 3, 4]))
// Prints 4

缺失的数字2

  • 很多成对出现的正整数保存在磁盘文件中，注意成对的数字不一定是相邻的，如 2，3，4，3，4，2……，如果有两个数字意外丢失了（丢失的不是相等的数字），该如何找到丢失的两个数字？

思路：设题目中这两个只出现 1 次的数字分别为 A 和 B，如果能将 A，B 分开到两个数组中，那显然符合“异或”解法的关键点了。因此这个题目的关键点就是将 A，B 分开到二个数组中。由于 A，B 肯定是不相等的，因此在二进制上必定有一位是不同的。根据这一位是 0 还是 1 可以将 A 和 B 分开到 A组 和 B组。而这个数组中其它数字要么属于 A 组，要么就属于 B 组。再对 A组 和 B组 分别执行“异或”解法就可以得到 A，B 了。而要判断 A，B 在哪一位上不相同，只要根据 “A异或B” 的结果就可以知道了，这个结果在二进制上为 1 的位都说明 A，B 在这一位上是不相同的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func findTwoLostNums(nums: [UInt]) -> (UInt, UInt) {
    var lostNum1: UInt = 0
    var lostNum2: UInt = 0
    var temp: UInt = 0
    //计算两个数的异或结果
    for num in nums {
        temp = temp ^ num
    }
    //找到第一个不为1的位
    var flag: UInt = 1;
    while ((flag & temp) == 0) {
        flag = flag << 1
    }
    //找两个丢失的数字
    for num in nums {
        if (num & flag == 0) {
            lostNum1 = lostNum1 ^ num
        } else {
            lostNum2 = lostNum2 ^ num
        }
    }
    return (lostNum1, lostNum2)
}
print(findTwoLostNums(nums: [1,2,1,3,2,4]))
// Prints (4, 3)

缺失的数字3

  • 数组中，只有一个数出现一次，剩下的都出现三次，找出出现一次的数字。

思路：考虑到三次异或后还是数字本身，所以不能像例2那样使用异或。根据位运算的思想，出现三次的数字每个比特位也出现了三次，如果将出现的次数相加的话，每一个比特位都可以被3整除。只出现一次的数字的每一个比特位出现的次数都是1，不能被3整除。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func findLostNum(nums: [UInt]) -> UInt {
    // 长度为32的数组
    var bitSum = [UInt](repeating: 0, count: 32)
    // 遍历二进制表示的32个比特位
    for i in 0..<32 {
        var sum: UInt = 0
        // 遍历数组，判断每个数的二进制表示，在第 i 位是否为1
        for num in nums {
            sum += (num >> i & 1)
        }
        // 保存所有数在第 i 位的总和
        bitSum[i] = sum
    }
    var res: UInt = 0
    for i in 0..<32 {
        // 不能被3整除的比特位，表示只出现一次的那个数字在这个二进制位上为1
        if (bitSum[i]%3 != 0) {
            // 将res的第i位置为1
            res += 1<<i
        }
    }
    return res
}
print(findLostNum(nums: [1,2,3,4,1,2,3,1,2,3]))
// Prints 4

运算符的优先升级和结核性

运算符的优先级使得一些运算符优先于其他运算符，高优先级的运算符会先被计算。

结合性定义了具有相同优先级的运算符是如何结合（或关联）的——与左边结合为一组，还是与右边结合为一组。

1
2
3
let c = 2 + 3 % 4 * 5
print(c)
// Prints 17

2 + 3 % 4 * 5 等价于 2 + ((3 % 4) * 5)。

运算符优先级 - 显示括号

Swift 语言中逻辑运算符 && 和 || 是做相关的，意味着多个逻辑运算符组合的表达式会首先计算最左边的子表达式。

1
2
3
4
5
6
7
8
let lockA = true, lockB = false, lockC = false, lockD = false
if (lockA && lockB || lockC || lockD) {
    print("Welcome!")
} else {
    print("ACCESS DENIED")
}
// Prints "ACCESS DENIED"

等价于

1
2
3
4
5
6
if ((lockA && lockB) || lockC || lockD) {
    print("Welcome!")
} else {
    print("ACCESS DENIED")
}
// Prints "ACCESS DENIED"

运算符重载

类和结构体可以为现有的运算符提供自定义的实现，称为运算符重载。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
struct Vector2D {
    var x = 0.0, y = 0.0
}
extension Vector2D {
    static func + (left: Vector2D, right: Vector2D) -> Vector2D {
        return Vector2D(x: left.x + right.x, y: left.y + right.y)
    }
}
let vector = Vector2D(x: 3.0, y: 1.0)
let anotherVector = Vector2D(x: 2.0, y: 4.0)
let combinedCector = vector + anotherVector
print(combinedCector)
// prints Vector2D(x: 5.0, y: 5.0)

一元运算符重载

类与结构体也能提供标准一元运算符的实现。要实现前缀或者后缀运算符，需要在声明运算符函数的时候在 func 关键字之前指定 prefix 或者 postfix 限定符。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
struct Vector2D {
    var x = 0.0, y = 0.0
}
extension Vector2D {
    static prefix func - (vector: Vector2D) -> Vector2D {
        return Vector2D(x: -vector.x, y: -vector.y)
    }
}
let positive = Vector2D(x: 3.0, y: 4.0)
let negative = -positive
let alsoPositive = -negative
print(negative)
print(alsoPositive)
// prints Vector2D(x: -3.0, y: -4.0)
// prints Vector2D(x: 3.0, y: 4.0)

组合赋值运算符重载

组合赋值运算符将赋值运算符（=）与其它运算符进行结合。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
struct Vector2D {
    var x = 0.0, y = 0.0
}
extension Vector2D {
    static func + (left: Vector2D, right: Vector2D) -> Vector2D {
        return Vector2D(x: left.x + right.x, y: left.y + right.y)
    }
}
extension Vector2D {
    // 把 left 设置成 inout 类型
    static func += (left: inout Vector2D, right: Vector2D) {
        left = left + right
    }
}
var original = Vector2D(x: 1.0, y: 2.0)
let vectorToAdd = Vector2D(x: 3.0, y: 4.0)
original += vectorToAdd
print(original)
// Prints Vector2D(x: 4.0, y: 6.0)

因为 left 的值会在运算符函数内直接被修改，所以需要把 left 设置成 inout 类型。

等价运算符重载

自定义类和结构体不接收等价运算符的默认实现，也就是所谓的“等于”运算符（==）和“不等于”运算符（!=）。要使用等价运算符，需要提供一个“等于”运算符（类似中缀运算符+），并且遵循标准库 Equaltable 协议。

1
2
3
4
5
6
7
8
9
10
struct Vector3D: Equatable {
    var x = 0.0, y = 0.0, z = 0.0
}
let vector01 = Vector3D(x: 2.0, y: 3.0, z: 4.0)
let vector02 = Vector3D(x: 2.0, y: 3.0, z: 4.0)
if vector01 == vector02 {
    print("vector01 == vector02")
}
// Prints "vector01 == vector02"

swift 为一下自定义类型提供等价运算符合成实现：

  • 只拥有遵循 Equaltable 协议存储属性的结构体
  • 只拥有遵循 Equaltable 协议关联类型的枚举
  • 没有关联类型的枚举

自定义运算符

除了实现标准运算符，在 Swift 中还可以声明和实现自定义运算符。自定义的运算符如果想在全局作用域内，可以使用 operator 关键字进行声明，同时还要指定 prefix、infix 或者 postfix 限定符。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// 全局作用域
prefix operator +++
struct Vector2D {
    var x = 0.0, y = 0.0
}
extension Vector2D {
    static func + (left: Vector2D, right: Vector2D) -> Vector2D {
        return Vector2D(x: left.x + right.x, y: left.y + right.y)
    }
}
extension Vector2D {
    static func += (left: inout Vector2D, right: Vector2D) {
        left = left + right
    }
}
// 自定义前缀翻倍运算符
extension Vector2D {
    static prefix func +++ (vector: inout Vector2D) -> Vector2D {
        vector += vector
        return vector
    }
}
var toBeDoubled = Vector2D(x: 1.0, y: 4.0)
let afterDoubling = +++toBeDoubled
print(afterDoubling)
// Prints Vector2D(x: 2.0, y: 8.0)

自定义中缀运算符的优先级和结合性

自定义的中缀（infix）运算符也可以指定优先级和结合性，每一个自定义的中缀运算符都属于一个优先级组，优先级组制定了自定义中缀运算符和其他中缀运算符的关系。

  • AdditionPrecedence 加法运算优先级组
  • MultiplicationPrecedence 乘法运算优先级组
1
2
3
4
5
6
7
// 自定义优先级组
precedencegroup MyPrecedence {
    // 设置优先级组的计算方向为从左侧开始
    associativity: left
    // 设置优先级小于加法运算优先级组
    lowerThan: AdditionPrecedence
}

自定义中缀运算符 +-

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
struct Vector2D {
    var x = 0.0, y = 0.0
}
// 自定义运算符 +- 属于加法运算符组
infix operator +-: AdditionPrecedence
extension Vector2D {
    static func +- (left: Vector2D, right: Vector2D) -> Vector2D {
        return Vector2D(x: left.x + right.x, y: left.y - right.y)
    }
}
// 自定义运算符 *^ 属于乘法运算符组
infix operator *^: MultiplicationPrecedence
extension Vector2D {
    static func *^ (left: Vector2D, right: Vector2D) -> Vector2D {
        return Vector2D(x: left.x * right.x, y: left.y * left.y + right.y + right.y)
    }
}
let firstVector = Vector2D(x: 1.0, y: 2.0)
let secondVector = Vector2D(x: 3.0, y: 7.0)
let plusMinusVector = firstVector +- secondVector
let thirdVector = Vector2D(x: 2.0, y: 2.0)
let resFirstVector = firstVector +- secondVector *^ thirdVector
let resSecondVector = (firstVector +- secondVector) *^ thirdVector
print(resFirstVector)
print(resSecondVector)
// Prints Vector2D(x: 7.0, y: -51.0)
// Prints Vector2D(x: 8.0, y: 29.0)

自定义运算符 +- 属于加法运算符组，自定义运算符 *^ 属于乘法运算符组。因为乘法运算的优先级大于加法运算，所以运算符组 +- 的优先级小于运算符组 \*^ ，即 \*^ 先于 +- 运算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
struct Vector2D {
    var x = 0.0, y = 0.0
}
// 自定义运算符 +- 属于加法运算符组
infix operator +-: AdditionPrecedence
extension Vector2D {
    static func +- (left: Vector2D, right: Vector2D) -> Vector2D {
        return Vector2D(x: left.x + right.x, y: left.y - right.y)
    }
}
infix operator
// 自定义运算符 *^ 属于乘法运算符组
precedencegroup MyPrecedence {
    // 设置优先级组的计算方向为从左侧开始
    associativity: left
    // 设置优先级小于加法运算优先级组
    lowerThan: AdditionPrecedence
}
extension Vector2D {
    static func *^ (left: Vector2D, right: Vector2D) -> Vector2D {
        return Vector2D(x: left.x * right.x, y: left.y * left.y + right.y + right.y)
    }
}
let firstVector = Vector2D(x: 1.0, y: 2.0)
let secondVector = Vector2D(x: 3.0, y: 7.0)
let plusMinusVector = firstVector +- secondVector
let thirdVector = Vector2D(x: 2.0, y: 2.0)
let resFirstVector = firstVector +- secondVector *^ thirdVector
let resSecondVector = (firstVector +- secondVector) *^ thirdVector
print(resFirstVector)
print(resSecondVector)
// Prints Vector2D(x: 7.0, y: -51.0)
// Prints Vector2D(x: 8.0, y: 29.0)

自定义运算符组 MyPrecedence，设置优先级低于加法运算组。即 *^ 和 +- 的执行顺序按从左至右的顺序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
struct Vector2D {
    var x = 0.0, y = 0.0
}
infix operator +-: AdditionPrecedence
extension Vector2D {
    static func +- (left: Vector2D, right: Vector2D) -> Vector2D {
        return Vector2D(x: left.x + right.x, y: left.y - right.y)
    }
}
//infix operator *^: MultiplicationPrecedence
infix operator *^: MyPrecedence
precedencegroup MyPrecedence {
    associativity: left
    lowerThan: AdditionPrecedence
}
extension Vector2D {
    static func *^ (left: Vector2D, right: Vector2D) -> Vector2D {
        return Vector2D(x: left.x * right.x, y: left.y * left.y + right.y + right.y)
    }
}
let firstVector = Vector2D(x: 1.0, y: 2.0)
let secondVector = Vector2D(x: 3.0, y: 7.0)
let plusMinusVector = firstVector +- secondVector
let thirdVector = Vector2D(x: 2.0, y: 2.0)
let resFirstVector = firstVector +- secondVector *^ thirdVector
let resSecondVector = (firstVector +- secondVector) *^ thirdVector
print(resFirstVector)
print(resSecondVector)
// Prints Vector2D(x: 8.0, y: 29.0)
// Prints Vector2D(x: 8.0, y: 29.0)